题目内容
18.计算(1)(-1)2+($\frac{1}{2}$)-1-5÷(2010-π)0
(2)$\frac{y}{{x}^{2}-xy}$+$\frac{x+y}{2x-2y}$
(3)(2ab2c-3)-2÷(a-2b)3
(4)$\frac{{x}^{2}}{x-y}$-x+y.
分析 根据分式的加减法,实数的运算方法,整式的除法,以及零指数幂和负整指数幂的运算方法,逐个题目计算即可.
解答 解:(1)(-1)2+($\frac{1}{2}$)-1-5÷(2010-π)0
=1+2-5
=-2
(2)$\frac{y}{{x}^{2}-xy}$+$\frac{x+y}{2x-2y}$
=$\frac{2y}{2{(x}^{2}-xy)}$+$\frac{{(x+y)}^{2}}{2{(x}^{2}-xy)}$
=$\frac{2y{+(x+y)}^{2}}{2{(x}^{2}-xy)}$
(3)(2ab2c-3)-2÷(a-2b)3
=$\frac{1}{4}$a-2b-4c6÷a-6b3
=$\frac{1}{4}$a4b-7c6
(4)$\frac{{x}^{2}}{x-y}$-x+y
=$\frac{{x}^{2}}{x-y}$-$\frac{{(x-y)}^{2}}{x-y}$
=$\frac{2xy{-y}^{2}}{x-y}$
点评 此题主要考查了分式的加减法,整式的除法,以及零指数幂和负整指数幂的运算方法,要熟练掌握.

练习册系列答案
相关题目
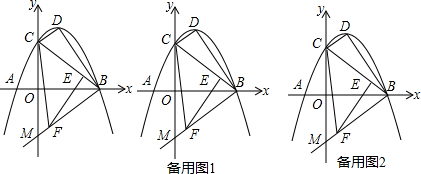
 如图,抛物线y=-x2+5x+n经过点A(1,0),与y轴交于点B.
如图,抛物线y=-x2+5x+n经过点A(1,0),与y轴交于点B.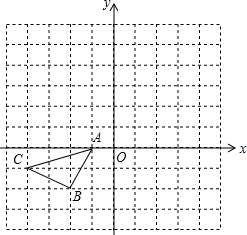 在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题.
在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题.