题目内容
1.把两个三角形按如图1放置,其中∠ACB=∠DEC=90°,∠CAB=45°,∠CDE=30°,且AB=6,DC=7,把△DCE绕点C顺时针旋转15°得△D1CE1,如图2,这时AB与CD1相交于点O,与D1E1相交于点F.
(1)求∠ACD1的度数;
(2)求线段AD1的长.
分析 (1)根据旋转的性质得出∠BCE1=15°,进而求出∠D1CB的度数,进而得出答案;
(2)根据已知得出OD1的长,进而利用勾股定理得出答案.
解答  解:(1)∵把△DCE绕点C顺时针旋转15°得△D1CE1,
解:(1)∵把△DCE绕点C顺时针旋转15°得△D1CE1,
∴∠BCE1=15°,
∴∠D1CB=60°-15°=45°,
∴∠AC D1=45°;
(2)∵∠AC D1=∠BC D1=45°
且AC=CB∴AO=BO=$\frac{1}{2}$AB=3,C D1⊥AB
∴CO=$\frac{1}{2}$AB=3∴O D1=7-3=4
在Rt△AO D1中有AO2+O D12=A D12
∴A D1=$\sqrt{{3}^{2}+{4}^{2}}$=5.
点评 此题主要考查了旋转的性质以及勾股定理等知识,根据已知得出O D1的长是解题关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
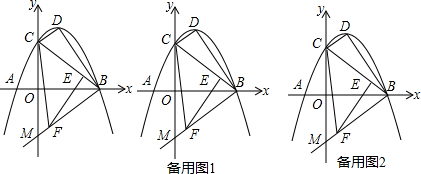
 如图,抛物线y=-x2+5x+n经过点A(1,0),与y轴交于点B.
如图,抛物线y=-x2+5x+n经过点A(1,0),与y轴交于点B.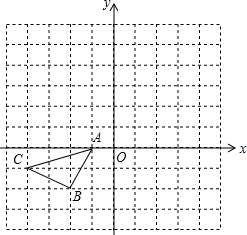 在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题.
在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题.