题目内容
17. 如图,直线y=$\frac{1}{3}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{3}$x向上平移$\frac{16}{3}$个长度单位后,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B.若SABO=16,则k的值为12.
如图,直线y=$\frac{1}{3}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{3}$x向上平移$\frac{16}{3}$个长度单位后,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B.若SABO=16,则k的值为12.
分析 作AM⊥x轴于M,BN⊥x轴于N,交OA于C,设A(x1,y1),B(x2,y2),SABO=$\frac{1}{2}$(y1+y2)•(x1-x2)=16,得出x1y2-x2y1=32,然后根据△ONC∽△OMA,对应边成比例得出x1y2-x2y1=$\frac{16}{3}$x1,从而得出$\frac{16}{3}$x1=32,求得A的坐标,即可求得k的值.
解答  解:∵直线y=$\frac{1}{3}$x向上平移$\frac{16}{3}$个长度单位后的解析式为y=$\frac{1}{3}$x+$\frac{16}{3}$,
解:∵直线y=$\frac{1}{3}$x向上平移$\frac{16}{3}$个长度单位后的解析式为y=$\frac{1}{3}$x+$\frac{16}{3}$,
作AM⊥x轴于M,BN⊥x轴于N,交OA于C,
设A(x1,y1),B(x2,y2),
∵SABO=$\frac{1}{2}$(y1+y2)•(x1-x2)=16,
∴x1y1-x2y1+x1y2-x2y2=32,
∵A、B是双曲线y=$\frac{k}{x}$(k>0,x>0)上的点,
∴k=x1y1=x2y2,
∴x1y2-x2y1=32,
∴AM∥BN,
∴△ONC∽△OMA,
∴$\frac{{x}_{2}}{{x}_{1}}$=$\frac{{y}_{2}-\frac{16}{3}}{{y}_{1}}$,
∴x1y2-x2y1=$\frac{16}{3}$x1,
∴$\frac{16}{3}$x1=32,
∴x1=6,
把x=6代入y=$\frac{1}{3}$x得,y=$\frac{1}{3}$×6=2,
∴A(6,2),
∴k=6×2=12.
故答案为12.
点评 本题考查了一次函数和反比例函数的交点问题,求得三角形AOB的面积等于梯形ABNM的面积是本题的关键.

练习册系列答案
相关题目
8.根据表中二次函数y=ax2+bx+c(a≠0)的自变量x与函数y的对应值,可判断该二次函数的图象与x轴的交点情况是( )
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -1 | -$\frac{7}{4}$ | -2 | -$\frac{7}{4}$ | … |
| A. | 只有一个交点 | B. | 有两个交点,且它们均在y轴同侧 | ||
| C. | 无交点 | D. | 有两个交点,且它们分别在y轴两侧 |
5.抛物线y=x2+2x-1的顶点坐标是( )
| A. | (1,2) | B. | (-1,-2) | C. | (1,-2) | D. | (-1,2) |
7.一元二次方程x2-4x+5=0的根的情况是( )
| A. | 没有实数根 | B. | 只有一个实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
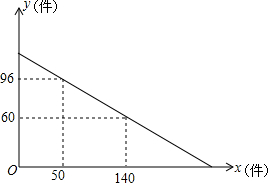 某服装店老板到批发中心批发A,B两种新款上衣,A种上衣的进货单价是B种上衣进货单价的1.5倍,考虑到各种因素,预计批发A种上衣数量y(件)与B种上衣的数量x(件)之间的函数关系如图所示,已知若批发的A,B 两种上衣中,A种有80件时,A,B两种上衣共需16800元.
某服装店老板到批发中心批发A,B两种新款上衣,A种上衣的进货单价是B种上衣进货单价的1.5倍,考虑到各种因素,预计批发A种上衣数量y(件)与B种上衣的数量x(件)之间的函数关系如图所示,已知若批发的A,B 两种上衣中,A种有80件时,A,B两种上衣共需16800元.  周末,东东一家三口人开车去距家15km的二克山公园游玩,行驶10min后,接到爷爷奶奶的电话,也要一同前往,于是妈妈下午步行前往,东东和爸爸开车按原路返回接爷爷奶奶,接到爷爷奶奶后,开车前往公园,在距离公园3.75km处追上妈妈并同车前往公园,若汽车速度始终保持不变,设汽车与家相距y1(单位:km),妈妈与家相距y2(单位:km),汽车离开家的时间为x(单位:min),y1、y2与x之间的函数图象如图所示,结合图象解答下列问题:
周末,东东一家三口人开车去距家15km的二克山公园游玩,行驶10min后,接到爷爷奶奶的电话,也要一同前往,于是妈妈下午步行前往,东东和爸爸开车按原路返回接爷爷奶奶,接到爷爷奶奶后,开车前往公园,在距离公园3.75km处追上妈妈并同车前往公园,若汽车速度始终保持不变,设汽车与家相距y1(单位:km),妈妈与家相距y2(单位:km),汽车离开家的时间为x(单位:min),y1、y2与x之间的函数图象如图所示,结合图象解答下列问题: