Question

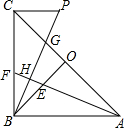如图，等腰Rt△ABC中，O为斜边AC的中点，∠CAB的平分线分别交BO，BC于点E，F，BP⊥AF于H，PC⊥BC，AE=1，PG=

 

．

Answer 1

考点：全等三角形的判定与性质,勾股定理,相似三角形的判定与性质

专题：

分析：可先证得△AEO∽△AFB，可求得AF和EF，再证明△BCG≌△AEB，可得AE=BG，再证明△BPC≌△ABF，可得BP=AF，可求得PG=EF，可求得答案．

解答：解：∵O为AC中点，
∴∠EOA=∠FBA=90°，
∵AF平分∠BAC，
∴∠OAE=∠FAB，
∴△AEO∽△AFB，
设OA=x，则AB=

2

x，
∴

AO

AB

=

AE

AF

，即

x

2 x

=

1

AF

，
∴AF=

2

，

∵△ABC为等腰三角形，O为AC中点
∴BC=BA，∠BCG=∠EBA=45°，
∵BP⊥AF，
∴∠CBG+∠PBA=∠EAB+∠PBA=90°，
∴∠CBG=∠EAB，
在△BCG和△AEB中，

∠BCG=∠EBA BC=BA ∠CBG=EAB

，
∴△BCG≌△AEB（ASA），
∴AE=BG=1，
∵PC⊥BC，
∴∠PCB=∠ABC=90°，
在△PBC和△FAB中，

∠PCB=∠FBA BC=BA ∠PBC=∠FAB

，
∴△PBC≌△FAB（ASA），
∴PB=AF=

2

，
∴PC=PB-BG=

2

-1，
故答案为：

2

-1．

点评：本题主要考查相似三角形、全等三角形的判定和性质，掌握相似三角形的边对应成比例、全等三角形的边相等是解题的关键．