题目内容
1.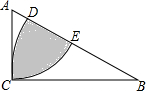 如图,在Rt△ABC中,∠A=60°,AB=2,以点B为圆心,BC为半径的弧交AB于点D,以点A为圆心,AC为半径的弧交AB于点E,则图中阴影部分的面积为$\frac{5π-6\sqrt{3}}{12}$.
如图,在Rt△ABC中,∠A=60°,AB=2,以点B为圆心,BC为半径的弧交AB于点D,以点A为圆心,AC为半径的弧交AB于点E,则图中阴影部分的面积为$\frac{5π-6\sqrt{3}}{12}$.
分析 根据扇形的面积公式:S=$\frac{nπ{R}^{2}}{360}$分别计算出S扇形ACE,S扇形BCD,并且求出三角形ABC的面积,最后由S阴影部分=S扇形ACE+S扇形BCD-S△ABC即可得到答案.
解答 解:S阴影部分=S扇形ACE+S扇形BCD-S△ABC,
∵S扇形ACE=$\frac{60π×1}{360}$=$\frac{π}{6}$,
S扇形BCD=$\frac{30π×3}{360}$=$\frac{π}{4}$,
S△ABC=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
∴S阴影部分=$\frac{π}{6}$+$\frac{π}{4}$-$\frac{\sqrt{3}}{2}$=$\frac{5π-6\sqrt{3}}{12}$.
故答案为$\frac{5π-6\sqrt{3}}{12}$.
点评 本题考查了扇形的面积公式:S=$\frac{nπ{R}^{2}}{360}$,其中n为扇形的圆心角的度数,R为圆的半径),或S=$\frac{1}{2}$lR,l为扇形的弧长,R为半径.

练习册系列答案
相关题目
11.若-$\frac{4(1-x)}{7}$的值是非正数,则x的取值范围是( )
| A. | x≤-1 | B. | x≥-1 | C. | x≥1 | D. | x≤1 |
6.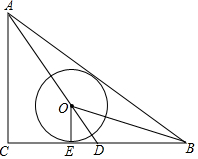 如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.
如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.
(1)求证:AB为⊙O的切线;
(2)求⊙O的半径;
(3)求tan∠BAD.
 如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.
如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.(1)求证:AB为⊙O的切线;
(2)求⊙O的半径;
(3)求tan∠BAD.
11.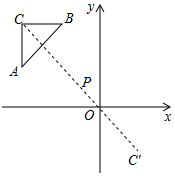 如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )
如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )
 如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )
如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )| A. | (2,0) | B. | (2,-1) | C. | (0,-2) | D. | (1,-2) |
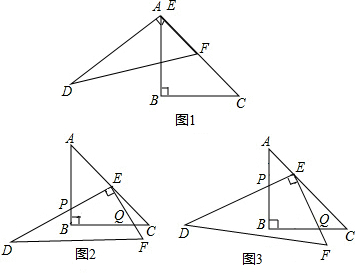
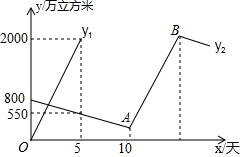 因南方旱情严重,乙水库的蓄水量以每天相同的速度持续减少,为缓解旱情,北方甲水库立即以管道运输的方式给予支援,如图是乙水库的蓄水量y1(单位:万立方米)关于时间x(单位:天)的函数图象和甲水库输水量y1(单位:万立方米)关于时间x(0≤x≤5)的函数图象,在单位时间内、甲水库的放水量与乙水库的进水量相同(水在排放、接收以及输送过程中的损耗不计),通过分析图象解答下列问题:
因南方旱情严重,乙水库的蓄水量以每天相同的速度持续减少,为缓解旱情,北方甲水库立即以管道运输的方式给予支援,如图是乙水库的蓄水量y1(单位:万立方米)关于时间x(单位:天)的函数图象和甲水库输水量y1(单位:万立方米)关于时间x(0≤x≤5)的函数图象,在单位时间内、甲水库的放水量与乙水库的进水量相同(水在排放、接收以及输送过程中的损耗不计),通过分析图象解答下列问题: