题目内容
16. 阅读下面的材料:
阅读下面的材料:在平面几何中,我们学过两条直线垂直的定义,下面就两个一次函数的图象所确定的两条直线,给出它们垂直的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1•k2=-1,我们就称直线l1与直线l2互相垂直.
解答下面的问题:
(1)求过点P(4,1)且与已知直线y=-2x-1垂直的直线l的函数表达式,并画出直线l的图象;
(2)设(1)中的直线l分别与y轴、x轴交于点A、B,如果直线m:y=kx+t(t<0)与直线l垂直且交x轴于点C,求△ABC的面积S关于t的函数表达式.
分析 (1)直线l与已知直线y=-2x-1平行,因而直线的一次项系数是$\frac{1}{2}$,根据待定系数法就可以求出函数解析式.
(2)点A、B的坐标可以求出,根据三角形的面积就可以求出C点的坐标.
解答 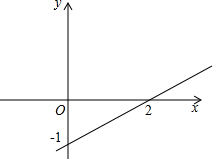 解:(1)设直线l的函数表达式为y=kx+b,
解:(1)设直线l的函数表达式为y=kx+b,
∵直线l与直线y=-2x-1垂直,
∴k=$\frac{1}{2}$,
∵直线l过点(4,1),
∴$\frac{1}{2}$×4+b=1,
∴b=-1.
∴直线l的函数表达式为y=$\frac{1}{2}$x-1.
直线l的图象如图;
(2)∵直线l分别与y轴、x轴交于点A、B,
∴点A、B的坐标分别为(0,-1)、(2,0).
∵l⊥m,
∴直线m为y=-2x+t.令y=0,解得x=$\frac{t}{2}$,
∴C点的坐标为($\frac{t}{2}$,0).
∵t<0,
∴$\frac{t}{2}$<0.
∴C点在x轴的负半轴上.
∴S=$\frac{1}{2}$×(2-$\frac{t}{2}$)×1=1-$\frac{t}{4}$;
△ABC的面积S关于t的函数表达式为S=1-$\frac{t}{4}$.
点评 本题主要考查了两直线相交或平行问题,待定系数法求函数的解析式,正确的求出函数解析式是解题的关键,.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
4.用配方法解方程x2-8x+15=0时,下列变形中,正确的是( )
| A. | (x-4)2=31 | B. | (x-4)2=1 | C. | (x-8)2=1 | D. | (x-8)2=31 |
11.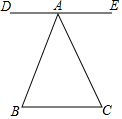 如图,ED∥BC,∠B=∠C,则下列正确的是( )
如图,ED∥BC,∠B=∠C,则下列正确的是( )
 如图,ED∥BC,∠B=∠C,则下列正确的是( )
如图,ED∥BC,∠B=∠C,则下列正确的是( )| A. | ∠BAE=∠DAC | B. | ∠BAE=∠ACB | C. | ∠ABC=∠DAC | D. | ∠BAC=∠DAC |
1.菱形ABCD的一边中点M到对角线交点O的距离为2.5cm,则菱形ABCD的周长为( )
| A. | 5 cm | B. | 10 cm | C. | 20 cm | D. | 40 cm |
