题目内容
 已知,如图:AB为⊙O直径,D为弧AC中点,DE⊥AB于E,AC交OD于点F,
已知,如图:AB为⊙O直径,D为弧AC中点,DE⊥AB于E,AC交OD于点F,(1)求证:OD∥BC;
(2)若AB=10cm,BC=6cm,求DF的长;
(3)探索DE与AC的数量关系,直接写出结论不用证明.
考点:垂径定理,勾股定理,圆周角定理
专题:证明题
分析:(1)根据圆周角定理,由AB为直径得到∠ACB=90°,再根据垂径定理,由D为弧AC中点得到OD⊥AC,则∠AFO=90°,于是根据平行线的判定方法即可得到OD∥BC;
(2)先判断OF为△ACB的中位线,则OF=
BC=3cm,然后利用DF=OD-OF求解;
(3)由OF为△ACB的中位线得到AF=CF,再证明△ODE≌△OAF,得到DE=AF,由此得到DE=
AC.
(2)先判断OF为△ACB的中位线,则OF=
| 1 |
| 2 |
(3)由OF为△ACB的中位线得到AF=CF,再证明△ODE≌△OAF,得到DE=AF,由此得到DE=
| 1 |
| 2 |
解答:(1)证明:∵AB为直径,
∴∠ACB=90°,
∵D为弧AC中点,
∴OD⊥AC,
∴∠AFO=90°,
∴OD⊥BC;
(2)解:∵OF∥BC,
而OA=OB,
∴OF为△ACB的中位线,
∴OF=
BC=3cm,
∴DF=OD-OF=5cm-3cm=2cm;
(3)解:DE=
AC.
∴∠ACB=90°,
∵D为弧AC中点,
∴OD⊥AC,
∴∠AFO=90°,
∴OD⊥BC;
(2)解:∵OF∥BC,
而OA=OB,
∴OF为△ACB的中位线,
∴OF=
| 1 |
| 2 |
∴DF=OD-OF=5cm-3cm=2cm;
(3)解:DE=
| 1 |
| 2 |
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理和三角形中位线性质.

练习册系列答案
相关题目
 如图,在数轴上点A表示的数可能是( )
如图,在数轴上点A表示的数可能是( )| A、2.6 | B、-2.6 |
| C、-1.8 | D、1.8 |
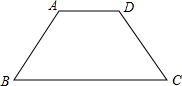 如图,在等腰梯形ABCD中,AD∥BC,∠C=60°,AD=6,AB=8,则BC=( )
如图,在等腰梯形ABCD中,AD∥BC,∠C=60°,AD=6,AB=8,则BC=( )| A、10 | B、12 | C、14 | D、16 |
 如图,在⊙O中,OD垂直于弦AB于点E,连接OB、CB,已知⊙O的半径为2,AB=
如图,在⊙O中,OD垂直于弦AB于点E,连接OB、CB,已知⊙O的半径为2,AB=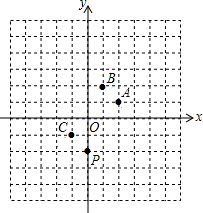 如图,在平面直角坐标系中,动点P从(0,-2)位置开始,一次关于点A、B、C作循环对称的跳动,即第一次跳到点P关于点A对称点M处,第二次接着跳到点M关于点B的对称点N处,第三次跳到点N关于点C的对称点处,…,按如此方法继续跳下去,则经过第2015次跳动之后,动点P落点处的坐标为
如图,在平面直角坐标系中,动点P从(0,-2)位置开始,一次关于点A、B、C作循环对称的跳动,即第一次跳到点P关于点A对称点M处,第二次接着跳到点M关于点B的对称点N处,第三次跳到点N关于点C的对称点处,…,按如此方法继续跳下去,则经过第2015次跳动之后,动点P落点处的坐标为 如图所示,A(-
如图所示,A(- 如图,在所画的两个雪人中,点A与点Aˊ,点B与点Bˊ,点C与点Cˊ是对应点,则AAˊ,BBˊ,CCˊ之间的关系是
如图,在所画的两个雪人中,点A与点Aˊ,点B与点Bˊ,点C与点Cˊ是对应点,则AAˊ,BBˊ,CCˊ之间的关系是