题目内容
 如图所示,A(-
如图所示,A(-| 3 |
考点:等边三角形的性质,坐标与图形性质
专题:
分析:过P点作PD⊥x轴,垂足为D,根据A(-
,0)、B(0,1)求OA、OB,利用勾股定理求AB,可得△ABC的面积,利用S△ABP=S△AOB+S梯形BODP-S△ADP,列方程求a.
| 3 |
解答:解:过P点作PD⊥x轴,垂足为D,
由A(-
,0)、B(0,1),得OA=
,OB=1,
∵△ABC为等边三角形,
由勾股定理,得AB=
=2,
∴S△ABC=
×2×
=
,
又∵S△ABP=S△AOB+S梯形BODP-S△ADP
=
×
×1+
×(1+a)×3-
×(
+3)×a,
=
,
由2S△ABP=S△ABC,得
+3-
a=
,
∴a=
.
故答案为:
.

由A(-
| 3 |
| 3 |
∵△ABC为等边三角形,
由勾股定理,得AB=
| OA2+OB2 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
| 3 |
又∵S△ABP=S△AOB+S梯形BODP-S△ADP
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
=
| ||||
| 2 |
由2S△ABP=S△ABC,得
| 3 |
| 3 |
| 3 |
∴a=
| 3 |
故答案为:
| 3 |
点评:本题考查了点的坐标与线段长的关系,不规则三角形面积的表示方法及等边三角形的性质和勾股定理.

练习册系列答案
相关题目
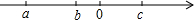 有理数a、b、c在数轴上的位置如图1所示,下面4个结论:①a+b<0;②b-c<0;③ac<0;④abc<0中,正确的个数是( )
有理数a、b、c在数轴上的位置如图1所示,下面4个结论:①a+b<0;②b-c<0;③ac<0;④abc<0中,正确的个数是( )| A、1个 | B、2个 |
| C、3 个 | D、4个 |
 如图,已知四边形ABCD中,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,则∠1+∠2=
如图,已知四边形ABCD中,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,则∠1+∠2= 如图,若?ABCD的对角线交于O,△OBC周长为59,BD为38,AC为24,△OBC比△OAB的周长多15,你能求出AD、AB的长是多少吗?
如图,若?ABCD的对角线交于O,△OBC周长为59,BD为38,AC为24,△OBC比△OAB的周长多15,你能求出AD、AB的长是多少吗? 已知,如图:AB为⊙O直径,D为弧AC中点,DE⊥AB于E,AC交OD于点F,
已知,如图:AB为⊙O直径,D为弧AC中点,DE⊥AB于E,AC交OD于点F, 如图:△ABC中,点O是AC边上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
如图:△ABC中,点O是AC边上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F. 如图,若?ABCD中,OA=5,OB=12,AC⊥BD,则AC=
如图,若?ABCD中,OA=5,OB=12,AC⊥BD,则AC= 下图(1)、(2)分别是
下图(1)、(2)分别是 已知l1∥l2∥l3,AB=3,DE=2,EF=4,求:AB和BC的长.
已知l1∥l2∥l3,AB=3,DE=2,EF=4,求:AB和BC的长.