题目内容
 如图,在⊙O中,OD垂直于弦AB于点E,连接OB、CB,已知⊙O的半径为2,AB=2
如图,在⊙O中,OD垂直于弦AB于点E,连接OB、CB,已知⊙O的半径为2,AB=2| 3 |
(1)OE的长度;
(2)∠BCD的度数.
考点:垂径定理,含30度角的直角三角形,勾股定理
专题:
分析:(1)根据垂径定理先求得EB,进而根据勾股定理即可求得OE的长;
(2)在直角三角形OEB中利用锐角三角函数求得∠EOB的度数,然后利用同弧所对的圆心角和圆周角之间的关系求得∠BCD的度数即可.
(2)在直角三角形OEB中利用锐角三角函数求得∠EOB的度数,然后利用同弧所对的圆心角和圆周角之间的关系求得∠BCD的度数即可.
解答:解:(1)∵直径CD垂直弦AB于点E,AB=2
,
∴EB=
AB=
,
∵⊙O的半径为2,
∴OB=2,
在RT△OBE中,OE=
=1;
(2)∵EB=
,OB=2,
∴sin∠EOB=
=
,
∴∠EOB=60°,
∴∠BCD=30°.
| 3 |
∴EB=
| 1 |
| 2 |
| 3 |
∵⊙O的半径为2,
∴OB=2,
在RT△OBE中,OE=
| OB2-EB2 |
(2)∵EB=
| 3 |
∴sin∠EOB=
| EB |
| OB |
| ||
| 2 |
∴∠EOB=60°,
∴∠BCD=30°.
点评:本题考查了垂径定理及特殊角的三角函数值,解题的关键是利用垂径定理得到直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
x2y3-3xy2-2次数和项数分别是( )
| A、5,3 | B、5,2 |
| C、2,3 | D、3,3 |
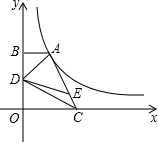 如图,点A在双曲线y=
如图,点A在双曲线y=| k |
| x |
A、
| ||
| B、3 | ||
C、
| ||
| D、1 |
 如图,数轴上有A、B、C、D四点,根据图中各点的位置,各点表示的数与5-
如图,数轴上有A、B、C、D四点,根据图中各点的位置,各点表示的数与5-| 30 |
| A、A | B、B | C、C | D、D |
 如图,已知四边形ABCD中,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,则∠1+∠2=
如图,已知四边形ABCD中,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,则∠1+∠2= 已知函数y=2x的图象为l1,函数y=2x-2的图象为l2.
已知函数y=2x的图象为l1,函数y=2x-2的图象为l2. 如图,若?ABCD的对角线交于O,△OBC周长为59,BD为38,AC为24,△OBC比△OAB的周长多15,你能求出AD、AB的长是多少吗?
如图,若?ABCD的对角线交于O,△OBC周长为59,BD为38,AC为24,△OBC比△OAB的周长多15,你能求出AD、AB的长是多少吗? 已知,如图:AB为⊙O直径,D为弧AC中点,DE⊥AB于E,AC交OD于点F,
已知,如图:AB为⊙O直径,D为弧AC中点,DE⊥AB于E,AC交OD于点F, 下图(1)、(2)分别是
下图(1)、(2)分别是