题目内容
如图，在所画的两个雪人中，点A与点Aˊ，点B与点Bˊ，点C与点Cˊ是对应点，则AAˊ，BBˊ，CCˊ之间的关系是考点：平移的性质
专题：
分析：根据平移的性质，对应点的连线平行且相等可得AA′∥BB′∥CC′，AA′=BB′=CC′．
解答：解：∵两个雪人可以看做一个雪人经过平移得到另一个雪人，点A与点Aˊ，点B与点Bˊ，点C与点Cˊ是对应点，
∴AA′∥BB′∥CC′，AA′=BB′=CC′，
∴AAˊ，BBˊ，CCˊ之间的关系是平行且相等，
故答案为：平行且相等．
∴AA′∥BB′∥CC′，AA′=BB′=CC′，
∴AAˊ，BBˊ，CCˊ之间的关系是平行且相等，
故答案为：平行且相等．
点评：本题考查了平移的性质，解题的关键是了解平移前后的两个图形的对应点的连线平行且相等．
练习册系列答案
阅读快车系列答案
相关题目
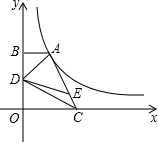如图，点A在双曲线y=| k |
| x |
A、
| ||
| B、3 | ||
C、
| ||
| D、1 |
已知，如图：AB为⊙O直径，D为弧AC中点，DE⊥AB于E，AC交OD于点F，
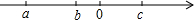有理数a、b、c在数轴上的位置如图1所示，下面4个结论：①a+b＜0；②b-c＜0；③ac＜0；④abc＜0中，正确的个数是（ ）| A、1个 | B、2个 |
| C、3 个 | D、4个 |
如图，若?ABCD中，OA=5，OB=12，AC⊥BD，则AC=
如图△ABC的三个顶点分别在2×3正方形方格的3个格点上，请你试着再在各点上找出三个点D、E、F，使得△DEF≌△ABC，这样的三角形一共有
下图（1）、（2）分别是估计下列各数（误差小于1）正确的是（ ）
A、
| |||
B、
| |||
C、
| |||
D、
|
如图，在△ABC中，AD=DE，AB=BE，∠A=70°，则∠DEC=