题目内容
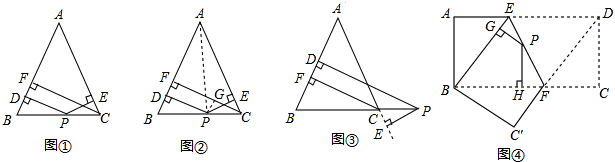
3. 如图:△ABC是等边三角形,以BD为边向外作等边三角形△DBC,点E,F分别在AB,AD上且AE=DF,连接BF,DE,两直线相交于点G,连接CG,下列结论:①∠BGE=60°,②CG平分∠BGD,③CG=DG+BG.其中正确的是( )
如图:△ABC是等边三角形,以BD为边向外作等边三角形△DBC,点E,F分别在AB,AD上且AE=DF,连接BF,DE,两直线相交于点G,连接CG,下列结论:①∠BGE=60°,②CG平分∠BGD,③CG=DG+BG.其中正确的是( )| A. | 仅有①③ | B. | 仅有①② | C. | 仅有②③ | D. | ①②③ |
分析 由三角形ABD为等边三角形,利用等边三角形的性质得到AB=BD,∠A=∠BDF=60°,再由AE=DF,利用SAS得到三角形AED与三角形DFB全等,利用全等三角形对应角相等得到∠ADE=∠DBF,利用三角形内角和定理及等边三角形性质得到∠BGE=60°;延长FB到点M,使BM=DG,连接CM.构建全等三角形△CDG≌△CBM,然后利用全等三角形的性质来证明CG=DG+BG,且得到GC为角平分线.
解答 解:∵△ABD为等边三角形,
∴AD=BD,∠A=∠BDF=60°,
在△AED和△DFB中,
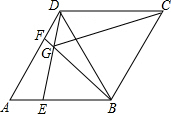
$\left\{\begin{array}{l}{AE=DF}\\{∠A=∠BDF}\\{AD=DB}\end{array}\right.$,
∴△AED≌△DFB(SAS),
∴∠ADE=∠DBF,
∵∠GEB=∠A+∠ADE=60°+∠ADE=60°+∠DBF,
∵∠DBF+∠GBE=60°,
∴∠BGE=180°-∠GEB-∠GBE=180°-60°-60°=60°,选项①正确;
延长FB到点M,使BM=DG,连接CM.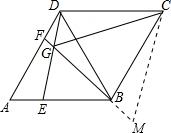
由(1)知,△AED≌△DFB,
∴∠ADE=∠DBF,
∵∠CDG=∠ADC-∠ADE=120°-∠ADE,∠CBM=120°-∠DBF.
∴∠CBM=∠CDG,
∵△DBC是等边三角形,
∴CD=CB,
在△CDG和△CBM中,
∵$\left\{\begin{array}{l}{CD=CB}\\{∠CDG=∠CBM}\\{DG=BM}\end{array}\right.$,
∴△CDG≌△CBM,
∴∠DCG=∠BCM,CG=CM,
∴∠GCM=∠DCB=60°,
∴△CGM是等边三角形,
∴CG=GM=BG+BM=BG+DG,选项③正确;
∵∠BGE=60°,
∴∠MGC=∠DGC=60°,即GC平分∠BGD,选项②正确
故选D.
点评 此题考查了全等三角形的判定与性质,以及等边三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案| A. | a+5<b+5 | B. | $\frac{a}{3}$<$\frac{b}{3}$ | C. | -4a>-4b | D. | 3a-2>3b-2 |
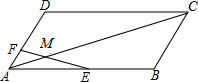 如图所示,在?ABCD中,AF:FD=1:3,E是AB中点,EF交AC于M,则AM:MC等于5.
如图所示,在?ABCD中,AF:FD=1:3,E是AB中点,EF交AC于M,则AM:MC等于5.