题目内容
13.已知关于x的方程kx2+(3k+1)x+3=0.(1)求证:无论k取任何实数时,方程总有实数根;
(2)若二次函数y=kx2+(3k+1)x+3的图象与x轴两个交点的横坐标均为整数,且k为整数,求k的值.
分析 (1)分类讨论:当k=0时,方程变形一元一次方程,有一个实数解;当k≠0时,计算判别式得到△=(3k-1)2,由此得到△≥0,由此判断当k≠0时,方程有两个实数根;
(2)先由求根公式得到kx2+(3k+1)x+3=0(k≠0)的解为x1=-$\frac{1}{k}$,x2=-3,则二次函数y=kx2+(3k+1)x+3的图象与x轴两个交点的横坐标分别为-$\frac{1}{k}$和-3,然后根据整数的整除性可确定整数k的值.
解答 (1)证明:当k=0时,方程变形为x+3=0,解得x=-3;
当k≠0时,△=(3k+1)2-4•k•3=(3k-1)2,
∵(3k-1)2≥0,
∴△≥0,
∴当k≠0时,方程有实数根,
∴无论k取任何实数时,方程总有实数根;
(2)解:kx2+(3k+1)x+3=0(k≠0)
x=$\frac{-(3k+1)±(3k-1)}{2k}$,
x1=-$\frac{1}{k}$,x2=-3,
所以二次函数y=kx2+(3k+1)x+3的图象与x轴两个交点的横坐标分别为-$\frac{1}{k}$和-3,
根据题意得-$\frac{1}{k}$为整数,
所以整数k为±1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了抛物线与x轴的交点.

练习册系列答案
相关题目
1.菱形的周长为4,两个相邻的内角的度数之比为1:2,则较短的对角线为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
18.为了应对期末考试,老师布置了15道选择题作业,批阅后得到如下统计表,根据表中数据可知,由45名学生答对题数组成的样本的中位数是14.
| 答对题数(道) | 12 | 13 | 14 | 15 |
| 人数 | 4 | 18 | 16 | 7 |
5.如果代数式$\frac{x-3}{\sqrt{x-2}}$有意义,那么x的取值范围是( )
| A. | x≥2 | B. | x>2且x≠3 | C. | x>2 | D. | x≥2且x≠3 |
2.点P(-1,3)向上平移1个单位长度后,再向左平移2个单位长度得到对应点Q,则Q点坐标是( )
| A. | (0,1) | B. | (-3,4) | C. | (2,1) | D. | (1,2) |
 如图,DE是△ABC的AB、AC两边中点的连线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S四边形ANME=1:5.
如图,DE是△ABC的AB、AC两边中点的连线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S四边形ANME=1:5.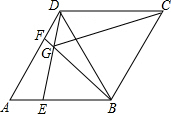 如图:△ABC是等边三角形,以BD为边向外作等边三角形△DBC,点E,F分别在AB,AD上且AE=DF,连接BF,DE,两直线相交于点G,连接CG,下列结论:①∠BGE=60°,②CG平分∠BGD,③CG=DG+BG.其中正确的是( )
如图:△ABC是等边三角形,以BD为边向外作等边三角形△DBC,点E,F分别在AB,AD上且AE=DF,连接BF,DE,两直线相交于点G,连接CG,下列结论:①∠BGE=60°,②CG平分∠BGD,③CG=DG+BG.其中正确的是( )