题目内容
12.若a>b,则下列不等式变形正确的是( )| A. | a+5<b+5 | B. | $\frac{a}{3}$<$\frac{b}{3}$ | C. | -4a>-4b | D. | 3a-2>3b-2 |
分析 根据不等式的性质1,可判断A;根据不等式的性质2,可判断B;根据不等式的性质3,可判断C,;根据不等式的性质1和2,可判断D.
解答 解:A、在不等式a>b的两边同时加上5,不等式仍成立,即a+5>b+5.故A选项错误;
B、在不等式a>b的两边同时除以3,不等式仍成立,即$\frac{a}{3}$<$\frac{b}{3}$.故B选项错误;
C、在不等式a>b的两边同时乘以-4,不等号方向改变,即-4a<-4b.故C选项错误;
D、在不等式a>b的两边同时乘以3,再减去2,不等式仍成立,即3a-2>3b-2.故D选项正确;
故选:D.
点评 本题主要考查了不等式的基本性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
相关题目
2.点P(-1,3)向上平移1个单位长度后,再向左平移2个单位长度得到对应点Q,则Q点坐标是( )
| A. | (0,1) | B. | (-3,4) | C. | (2,1) | D. | (1,2) |
3.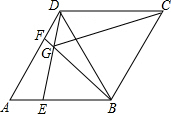 如图:△ABC是等边三角形,以BD为边向外作等边三角形△DBC,点E,F分别在AB,AD上且AE=DF,连接BF,DE,两直线相交于点G,连接CG,下列结论:①∠BGE=60°,②CG平分∠BGD,③CG=DG+BG.其中正确的是( )
如图:△ABC是等边三角形,以BD为边向外作等边三角形△DBC,点E,F分别在AB,AD上且AE=DF,连接BF,DE,两直线相交于点G,连接CG,下列结论:①∠BGE=60°,②CG平分∠BGD,③CG=DG+BG.其中正确的是( )
 如图:△ABC是等边三角形,以BD为边向外作等边三角形△DBC,点E,F分别在AB,AD上且AE=DF,连接BF,DE,两直线相交于点G,连接CG,下列结论:①∠BGE=60°,②CG平分∠BGD,③CG=DG+BG.其中正确的是( )
如图:△ABC是等边三角形,以BD为边向外作等边三角形△DBC,点E,F分别在AB,AD上且AE=DF,连接BF,DE,两直线相交于点G,连接CG,下列结论:①∠BGE=60°,②CG平分∠BGD,③CG=DG+BG.其中正确的是( )| A. | 仅有①③ | B. | 仅有①② | C. | 仅有②③ | D. | ①②③ |
7.菱形的两条对角线的长分别为6和8,则菱形的高为( )
| A. | $\frac{24}{5}$ | B. | $\frac{48}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{12}{5}$ |
1.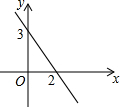 一次函数y=kx-k(k≠0)的图象如图所示,若y>0,则x的取值范围是( )
一次函数y=kx-k(k≠0)的图象如图所示,若y>0,则x的取值范围是( )
 一次函数y=kx-k(k≠0)的图象如图所示,若y>0,则x的取值范围是( )
一次函数y=kx-k(k≠0)的图象如图所示,若y>0,则x的取值范围是( )| A. | x<0 | B. | x>0 | C. | x>2 | D. | x<2 |