题目内容
14.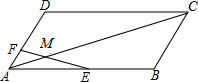 如图所示,在?ABCD中,AF:FD=1:3,E是AB中点,EF交AC于M,则AM:MC等于5.
如图所示,在?ABCD中,AF:FD=1:3,E是AB中点,EF交AC于M,则AM:MC等于5.
分析 延长FE交CB的延长线于G,利用已知条件证明△AFE≌△BGE,可得到AF=BG,再有平行线四边形的性质可证明△AFM∽△CGM,利用相似三角形的性质即可求出$\frac{CM}{MA}$的值.
解答 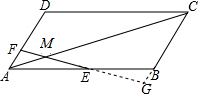 解:延长FE交CB的延长线于G,
解:延长FE交CB的延长线于G,
∵四边形ABCD是平行四边形,
∴∠EAF=∠GBE,∠AFE=∠BGE,
在△FFE与△BGE中,$\left\{\begin{array}{l}{∠EAF=∠GBE}\\{AE=BE}\\{∠AEF=∠BEG}\end{array}\right.$,
∴△AFE≌△BME,
∴AF=BG,
∵AF:FD=1:3,
∴AF:AD=1:4,
∴AF:GC=1:5,
∵AD∥BC,
∴△AFM∽△CGM,
∴AF:GC=AM:CM=1:5,
∴CM:AM=5:1=5,
故答案为:5.
点评 此题综合考查了平行四边形的性质、全等三角形的判定及性质、相似三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.如果代数式$\frac{x-3}{\sqrt{x-2}}$有意义,那么x的取值范围是( )
| A. | x≥2 | B. | x>2且x≠3 | C. | x>2 | D. | x≥2且x≠3 |
2.点P(-1,3)向上平移1个单位长度后,再向左平移2个单位长度得到对应点Q,则Q点坐标是( )
| A. | (0,1) | B. | (-3,4) | C. | (2,1) | D. | (1,2) |
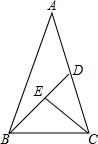 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E.设k=$\frac{\sqrt{5}-1}{2}$,则DE=$\frac{3-\sqrt{5}}{2}$a.
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E.设k=$\frac{\sqrt{5}-1}{2}$,则DE=$\frac{3-\sqrt{5}}{2}$a.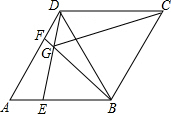 如图:△ABC是等边三角形,以BD为边向外作等边三角形△DBC,点E,F分别在AB,AD上且AE=DF,连接BF,DE,两直线相交于点G,连接CG,下列结论:①∠BGE=60°,②CG平分∠BGD,③CG=DG+BG.其中正确的是( )
如图:△ABC是等边三角形,以BD为边向外作等边三角形△DBC,点E,F分别在AB,AD上且AE=DF,连接BF,DE,两直线相交于点G,连接CG,下列结论:①∠BGE=60°,②CG平分∠BGD,③CG=DG+BG.其中正确的是( )