题目内容
如图，已知：AB为⊙O的直径，CD为⊙O的一条弦，BC与AD相交于点M，∠AMC=α，则S△CMD：S△ABM=考点：圆周角定理,相似三角形的判定与性质
专题：
分析：首先连接AC，由AB为⊙O的直径，根据直径所对的圆周角是直角，即可得在Rt△ACM中，cosα=
，易证得△CDM∽△ABM，然后由相似三角形面积比等于相似比的平方，即可求得S△CMD：S△ABM的值．
| CM |
| AM |
解答：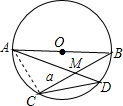
解：连接AC，
∵AB为⊙O的直径，
∴∠ACB=90°，
∴在Rt△ACM中，cosα=
，
∵∠B=∠D，∠BAD=∠BCD，
∴△CDM∽△ABM，
∴S△CMD：S△ABM=（
）2=cos2α．
故答案为：cos2α．
解：连接AC，∵AB为⊙O的直径，
∴∠ACB=90°，
∴在Rt△ACM中，cosα=
| CM |
| AM |
∵∠B=∠D，∠BAD=∠BCD，
∴△CDM∽△ABM，
∴S△CMD：S△ABM=（
| CM |
| AM |
故答案为：cos2α．
点评：此题考查了圆周角定理、相似三角形的判定与性质以及三角函数定义．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A1，作正方形A1B1C1C；延长C1B1交x轴于点A2，作正方形A2B2C2C1…按这样的规律进行下去，正方形A2011B2011C2011C2010的面积为（ ）A、5×(
| ||
B、5×(
| ||
C、5×(
| ||
D、5×(
|
方程组
的解是（ ）
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
如图，DE∥BC，EF∥AB，若AE：AC=1：3，则DE：FC=