题目内容
已知直线y=﹣x+6,交x轴、y轴于A、B两点,抛物线y=x2+mx+n经过A点,且与直线y=﹣x+6交于另一点P.
(1)若P与B点重合,求抛物线的解析式;
(2)若P在第一象限,过PE⊥x轴于E点,PF⊥y轴于F点,当四边形PEOF面积为5,求抛物线的解析式;
(3)若△OAP为等腰三角形,求m的值.


【考点】二次函数综合题.
【分析】(1)分别令x、y=0,可求出B、A点的坐标,再利用待定系数法即可得出结论;
(2)由四边形PEOF面积为5可得出P点的坐标,结合A点的坐标利用待定系数法即可求得结论;
(3)设出P点坐标,由两点间的距离公式表示出△OAP的三条边,再分类讨论相邻两边相等得出结论.
【解答】解:(1)令x=0,则y=6;
令y=0,则﹣x+6=0,解得:x=6.
故A点坐标为(6,0),B点坐标为(0,6).
∵P与B点重合,
∴有
 ,解得:
,解得:
 .
.
故当P与B点重合,抛物线的解析式为y=x2﹣7x+6.
(2)结合题意画出图形,如图1所示.


∵点P在线段AB上,
∴设P点坐标为(a,﹣a+6)(0<m<6),则有PE=6﹣m,PF=m.
四边形PEOF面积=PE•PF=(6﹣a)×a=5,
解得:a=1,或a=5,
即点P的坐标为(1,5)或(5,1).
当点P坐标为(1,5)时,有
 ,
,
解得:
 ,
,
此时抛物线的解析式为y=x2﹣8x+12;
当点P坐标为(5,1)时,有
 ,
,
解得:
 ,
,
此时抛物线的解析式为y=x2﹣12x+36.
综上可知,抛物线的解析式为y=x2﹣8x+12或者y=x2﹣12x+36.
(3)设点P的坐标为(b,6﹣b).
∵点O(0,0),点A(6,0),
∴OP=
 ,OA=6﹣0=6,PA=
,OA=6﹣0=6,PA=
 .
.
∵△OAP为等腰三角形,
∴分三种情况考虑.
①当OP=OA时,有
 =6,
=6,
解得:b=0,或b=6(舍去),
此时P点的坐标为(0,6).
同(1)一样,故m=﹣7;
②当OP=PA,即
 =
=
 ,
,
解得:b=3,
此时P点的坐标为(3,3).
将P(3,3),A(6,0)代入抛物线解析式,得:

 ,解得m=﹣10;
,解得m=﹣10;
③当OA=PA时,有6=
 ,
,
解得:b=6±3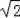
 ,
,
此时P点的坐标为(6+3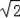
 ,﹣3
,﹣3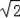
 )或(6﹣3
)或(6﹣3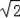
 ,3
,3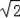
 ).
).
将P(6+3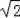
 ,﹣3
,﹣3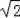
 ),A(6,0)代入抛物线解析式,得:
),A(6,0)代入抛物线解析式,得:

 ,解得m=﹣3
,解得m=﹣3
 ﹣13;
﹣13;
将P(6﹣3
 ,3
,3
 ),A(6,0)代入抛物线解析式,得:
),A(6,0)代入抛物线解析式,得:

 ,解得m=3
,解得m=3
 ﹣13.
﹣13.
综上可知:当△OAP为等腰三角形,m的值为﹣7,﹣10,﹣3
 ﹣13和3
﹣13和3
 ﹣13.
﹣13.
【点评】本题考查了待定系数法求函数的解析式、长方形的面积公式、两点间的距离公式以及解一元二次方程,解题的关键:(1)利用待定系数法求函数解析式;(2)利用长方形的面积找出P点的坐标;(3)由两点间的距离公式分类讨论相邻两边相等的情况.本题属于中档题,(1)(2)难度不大,(3)难度也不大,单运算过程很繁琐,这就需要极大的耐心一步步运算.






 的相反数是
的相反数是 



 的解适合x+y=8,求m的值.
的解适合x+y=8,求m的值.