题目内容
在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=40°,∠B=60°
C.∠A=20°,∠B=80° D.∠A=40°,∠B=80°
C【考点】等腰三角形的判定.
【分析】根据等腰三角形性质,利用三角形内角定理对4个选项逐一进行分析即可得到答案.
【解答】解;当顶角为∠A=40°时,∠C=70°≠50°,
当顶角为∠B=50°时,∠C=65°≠40°
所以A选项错误.
当顶角为∠B=60°时,∠A=60°≠40°,
当∠A=40°时,∠B=70°≠60°,
所以B选项错误.
当顶角为∠A=40°时,∠C=70°=∠B,
所以C选项正确.
当顶角为∠A=40°时,∠B=70°≠80°,
当顶角为∠B=80°时,∠A=50°≠40°
所以D选项错误.
故选C.
【点评】此题主要考查学生对等腰三角形的性质和三角形内角和定理的理解和掌握,解答此题的关键是熟练掌握三角形内角和定理.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目



 (m≠0,x>0)分别交于D、E两点,若点D的坐标为(4,1),点E的坐标为(1,n)
(m≠0,x>0)分别交于D、E两点,若点D的坐标为(4,1),点E的坐标为(1,n)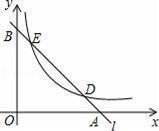


 有意义的x的取值范围是
有意义的x的取值范围是 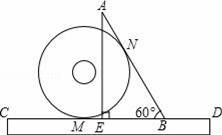


 AB时,求tan∠CED的值;
AB时,求tan∠CED的值;


