题目内容
牧场上有一片牧草供24头牛六周吃完,供18头牛十周吃完,假定草的生长速度不变,那么供19头牛需要几周吃完?
考点:应用类问题
专题:
分析:根据题意利用18头牛吃10周的草量以及24头牛吃6周的草量和19头牛x周所吃的草量得出等式求出即可.
解答:解:设一头牛一周吃草量为a,草场每周草的生长量为b,这片牧场原有草量为c,十九头牛需要x周吃完,得:
,
由②-①,得b=9a④,
由③-①,得(x-6)b=(19x-144)a⑤,
将④代入⑤得:(x-6)•9a=(19x-144)a,
∵a≠0,
∴9(x-6)=19x-144,
解得:x=9,
故供19头牛需要9周吃完.
|
由②-①,得b=9a④,
由③-①,得(x-6)b=(19x-144)a⑤,
将④代入⑤得:(x-6)•9a=(19x-144)a,
∵a≠0,
∴9(x-6)=19x-144,
解得:x=9,
故供19头牛需要9周吃完.
点评:此题主要考查了应用类问题,利用牛的吃草量得出等式是解题关键.

练习册系列答案
相关题目
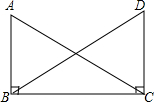 如图所示,已知AB=DC,∠ABC=∠DCB=90°,可以推得Rt△ABC≌Rt△DCB,所用的判断定理简称是( )
如图所示,已知AB=DC,∠ABC=∠DCB=90°,可以推得Rt△ABC≌Rt△DCB,所用的判断定理简称是( )| A、SAS | B、HL |
| C、ASA | D、AAS |
已知
-
=1,则
的值( )
| 1 |
| a |
| 1 |
| b |
| a-ab-b |
| 3a+ab-3b |
| A、1 | B、2 | C、3 | D、4 |
 如图,⊙O的直径AB经过弦CD的中点,∠BAC=20°,则∠BOD等于( )
如图,⊙O的直径AB经过弦CD的中点,∠BAC=20°,则∠BOD等于( )| A、10° | B、20° |
| C、40° | D、80° |
 如图,反比例函数y=
如图,反比例函数y=