题目内容
某商店以每件5元的价格购进一种文具,由试销知,该文具每天的销售量t与每件的销售价x之间满足一次函数t=-x+13.
(1)写出商店每天销售这种文具的毛利润y与每件的销售价x之间的函数关系式;
(2)商店要想每天获得最大销售毛利润,每件的销售价应定为多少元?最大销售毛利润为多少元?
(1)写出商店每天销售这种文具的毛利润y与每件的销售价x之间的函数关系式;
(2)商店要想每天获得最大销售毛利润,每件的销售价应定为多少元?最大销售毛利润为多少元?
考点:二次函数的应用
专题:
分析:(1)利用毛利润=每一件的销售利润×销售量列出函数解析式即可;
(2)利用(1)中解析式,运用配方法求得答案即可.
(2)利用(1)中解析式,运用配方法求得答案即可.
解答:解:(1)y=(x-5)(-x+13)=-x2+18x-65,
所以商店每天销售这种文具的毛利润y与每件的销售价x之间的函数关系式是y=-x2+18x-65.
(2)y=-x2+18x-65=-(x-9)2+16,
即每件的销售价应定为9元,最大销售毛利润为16元.
所以商店每天销售这种文具的毛利润y与每件的销售价x之间的函数关系式是y=-x2+18x-65.
(2)y=-x2+18x-65=-(x-9)2+16,
即每件的销售价应定为9元,最大销售毛利润为16元.
点评:此题考查二次函数的实际运用,理解题意,列出函数解析式是解决问题的关键.

练习册系列答案
相关题目
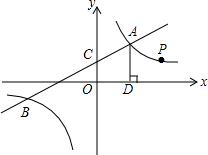 如图,一次函数y1=k1x+2与反比例函数y2=
如图,一次函数y1=k1x+2与反比例函数y2=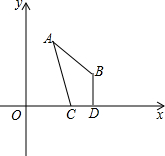 如图,平面直角坐标系中A(1,4),B(3,2),C、D为x轴上两动点,且CD=1,试求四边形ACDB周长最小时,C、D两点的坐标.
如图,平面直角坐标系中A(1,4),B(3,2),C、D为x轴上两动点,且CD=1,试求四边形ACDB周长最小时,C、D两点的坐标.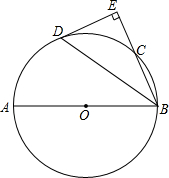 如图,AB是⊙O的直径,∠ABC的平分线BD交⊙O于D,过点D作DE⊥BC的延长线于点E.
如图,AB是⊙O的直径,∠ABC的平分线BD交⊙O于D,过点D作DE⊥BC的延长线于点E.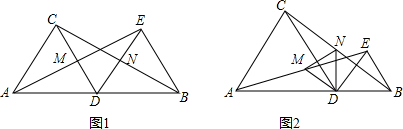
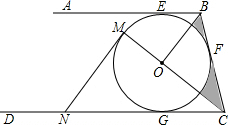 如图,AB、BC、CD分别于⊙O相切于E、F、G,且AB∥CD,连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
如图,AB、BC、CD分别于⊙O相切于E、F、G,且AB∥CD,连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.