题目内容
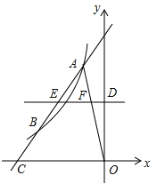
【题目】如图，已知抛物线与
轴交于
，
点，与
轴交于点
，抛物线的顶点为
，连接
．
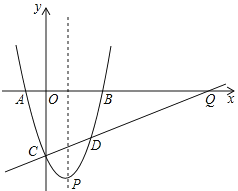
（1）求此抛物线的表达式；
（2）在抛物线上找一点
，使得
与垂直，且直线与轴交于点
，求点的坐标；
（3）抛物线对称轴上是否存在一点
，使得
，若存在，求出点坐标；若不存在，请说明理由．
【答案】（1）
（2）
（3）存在；
或
【解析】
（1）利用交点式将抛物线与x轴交于A（-1，0）、B（3，0）两点，代入y=a（x-x1）（x-x2），求出二次函数解析式即可；
（2）利用△QOC∽△COA，得出QO的长度，得出Q点的坐标，再求出直线QC的解析式，将两函数联立求出交点坐标即可；
（3）首先求出二次函数顶点坐标，由S四边形AEPC=S四边形OEPC+S△AOC以及S四边形AEPC=S△AEP+S△ACP，得出使得S△MAP=3S△ACP的点M的坐标．
解：（1）设此抛物线的表达式为
抛物线与
轴交于点
抛物线与
轴交于
，
两点
解得
此抛物线的表达式为
（2）
，
，
，
，
轴，
，
，
，
即
又点
在轴的正半轴上，
设直线
的表达式为
则
解得
直线的表达式为
：
点
是抛物线与直线的交点
解得
，
（不合题意舍去）
此时
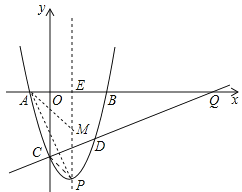
（3）对称轴；
此时
点
在直线
上，
设
，连接
、
、
直线与轴交于点
，
，
则
又
，
，
，
，
．
故对称轴上存在点使
，点的坐标为或．
【点晴】
本题主要考查了二次函数的综合应用，二次函数的综合应用是初中阶段的重点题型，特别注意利用数形结合是这部分考查的重点，也是难点．
练习册系列答案
学业测评一课一测系列答案
相关题目
