题目内容
【题目】已知二次函数![]() 与一次函数
与一次函数![]() ,
,
(1)求证:对任意的实数![]() ,函数
,函数![]() 与
与![]() 的图象总有两个交点;
的图象总有两个交点;
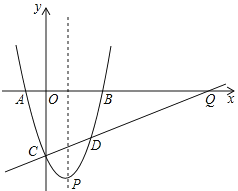
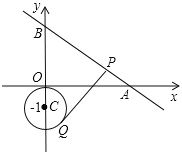
(2)设![]() 与
与![]() 的图象相交于
的图象相交于![]() 两点,
两点,![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() ,记
,记![]() 与
与![]() 的面积分别为
的面积分别为![]() (
(![]() 为坐标原点),求证:
为坐标原点),求证:![]() 总是定值;
总是定值;
(3)对于二次函数![]() ,是否存在实数
,是否存在实数![]() ,使得当
,使得当![]() 时,恰好有
时,恰好有![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)把两函数联立得到一元二次方程,根据根的判别式△>0即可求解;
(2)设![]() ,根据一元二次方程根与系数的关系得到
,根据一元二次方程根与系数的关系得到![]() ,再根据二次函数的解析式求出C点坐标,得到
,再根据二次函数的解析式求出C点坐标,得到![]() ,再代入
,再代入![]() 即可求解;
即可求解;
(3)先把二次函数化为顶点式,当![]() 时,
时,![]() 有最大值
有最大值![]() ,根据当
,根据当![]() 时,恰好有
时,恰好有![]() ,故
,故![]() ,而函数的对称轴为
,而函数的对称轴为![]() ,得到函数值会随着
,得到函数值会随着![]() 增大而增大,把(a,a)和(b,b)代入二次函数,再根据根与系数的关系得到
增大而增大,把(a,a)和(b,b)代入二次函数,再根据根与系数的关系得到![]() ,故可求出
,故可求出![]() 的值.
的值.
解:(1)联立![]() 与
与![]() 的方程
的方程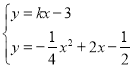
消去![]() 得
得![]()
![]()
![]() 对任意的实数
对任意的实数![]() ,函数
,函数![]() 与
与![]() 的图象总有两个交点.
的图象总有两个交点.
(2)设![]() ,则
,则![]() 是方程
是方程![]() 的两根,
的两根,
由根与系数的关系知:![]() ,因为二次函数
,因为二次函数![]() 与
与![]() 轴相交于点
轴相交于点![]()
所以![]()
故![]() 总是定值
总是定值![]() ;
;
(3)![]() ,当
,当![]() 时,
时,![]() 有最大值
有最大值![]() ,
,
所以![]() ,而函数的对称轴为
,而函数的对称轴为![]() ,
,
所以当![]() 时,
时,
函数值会随着![]() 增大而增大,
增大而增大,
把(a,a)和(b,b)代入二次函数得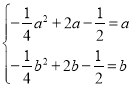 ,
,
则
所以![]() 是方程
是方程![]() 的两根且这两根均小于4,
的两根且这两根均小于4,
所以![]()
∴ .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某市一研究机构为了了解![]() 岁年龄段市民对创建文明城市的关注程度,随机选取了
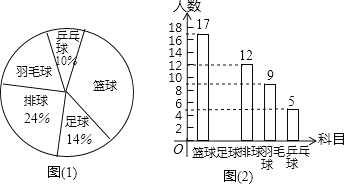
岁年龄段市民对创建文明城市的关注程度,随机选取了![]() 名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
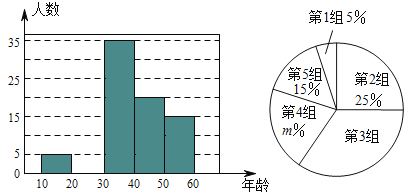
(1)请直接写出![]() ,第
,第![]() 组人数在扇形统计图中所对应的圆心角是 度;
组人数在扇形统计图中所对应的圆心角是 度;
(2)请补全上面的频数分布直方图:
(3)假设该市现有![]() 岁的市民
岁的市民![]() 万人,问
万人,问![]() 岁年龄段的关注创建文明城市的人数约有多少?
岁年龄段的关注创建文明城市的人数约有多少?