题目内容
16.若分式$\frac{2x+1}{{x}^{2}}$的值为正,则x的取值范围是( )| A. | x>0 | B. | x>-$\frac{1}{2}$ | C. | x≠-$\frac{1}{2}$ | D. | x>-$\frac{1}{2}$且x≠0 |
分析 根据题意,因为任何实数的平方都是非负数,分母有不能为0,所以分母必是正数,主要分子的值是正数则可,从而列出不等式.
解答 解:由题意得,x2≠0,
∴x≠0,
∵分式$\frac{2x+1}{{x}^{2}}$的值为正,
∴2x+1>0,
∴x>-$\frac{1}{2}$,
所以x>-$\frac{1}{2}$且x≠0.
故选:D.
点评 本题考查不等式的解法和分式值的正负条件.解不等式时当未知数的系数是负数时,两边同除以未知数的系数需改变不等号的方向,当未知数的系数是正数时,两边同除以未知数的系数不需改变不等号的方向.

练习册系列答案
相关题目
7.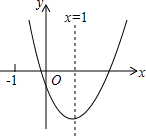 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )
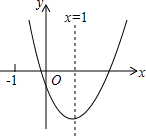 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )| A. | ①② | B. | ①④ | C. | ①③④ | D. | ②③④ |
4. 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a-b+c>0;
②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论是( )
 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a-b+c>0;
②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论是( )
| A. | ①②③ | B. | ①③④ | C. | ③④⑤ | D. | ②③⑤ |
11.已知$\frac{x+5}{16}$是一个最简真分数,那么x可以取的自然数有( )个.
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
1.下列数中与-2互为倒数的是( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
8.有些国家的国旗设计成了轴对称图形,观察如图代表国旗的图案,你认为是轴对称图形的有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
 如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于A、B两点,且与反比例函数y=$\frac{k_2}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OA=OB=2,OD=1.
如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于A、B两点,且与反比例函数y=$\frac{k_2}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OA=OB=2,OD=1. 如图,在△ABC中,∠ABC,∠ACB的平分线BD,CE相交于点O,若∠ABC=40°,∠ACB=60°,求∠BOC的大小.
如图,在△ABC中,∠ABC,∠ACB的平分线BD,CE相交于点O,若∠ABC=40°,∠ACB=60°,求∠BOC的大小.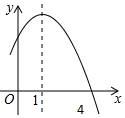 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为x1=4,x2=-2.
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为x1=4,x2=-2.