题目内容
15.不改变分式的值,使下列分式的分子和分母都不含“-“号.(1)$\frac{b}{-5a}$;
(2)$\frac{-abc}{-d}$;
(3)-$\frac{-3m}{2n}$;
(4)-$\frac{-2q}{-p}$.
分析 (1)有一个负号,分式的值为负;
(2)有两个负号,分式的值为正;
(3)有两个负号,分式的值为正;
(4)有三个负号,分式的值为负.
解答 解:(1)$\frac{b}{-5a}$=-$\frac{b}{5a}$;
(2)$\frac{-abc}{-d}$=$\frac{abc}{d}$;
(3)-$\frac{-3m}{2n}$=$\frac{3m}{2n}$;
(4)-$\frac{-2q}{-p}$=-$\frac{2q}{p}$.
点评 本题考查了分式的基本性质,不改变分式的值,使分式的分子和分母都不含“-“号,解题思路为:看分子、分母和分式的符号中有几个负号,若有奇数个时,分式为负,若有偶数个时,分式为正.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
3.若x=-1是关于x的方程2x+m=1的解,则m-1的值是( )
| A. | 3 | B. | 2 | C. | -2 | D. | -1 |
20.已知am=9,am-2n=3,则an的值是( )
| A. | -3 | B. | $\sqrt{3}$ | C. | $\frac{1}{3}$ | D. | ±$\sqrt{3}$ |
7.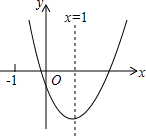 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )
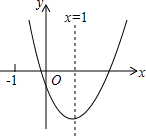 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )| A. | ①② | B. | ①④ | C. | ①③④ | D. | ②③④ |
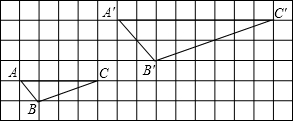
 如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于A、B两点,且与反比例函数y=$\frac{k_2}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OA=OB=2,OD=1.
如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于A、B两点,且与反比例函数y=$\frac{k_2}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OA=OB=2,OD=1.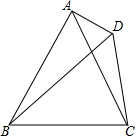 如图,△ABC是等边三角形,D是△ABC外一点,且∠BDC=60°,判断DA、DB、DC的数量关系.
如图,△ABC是等边三角形,D是△ABC外一点,且∠BDC=60°,判断DA、DB、DC的数量关系. 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论: 如图,在△ABC中,∠ABC,∠ACB的平分线BD,CE相交于点O,若∠ABC=40°,∠ACB=60°,求∠BOC的大小.
如图,在△ABC中,∠ABC,∠ACB的平分线BD,CE相交于点O,若∠ABC=40°,∠ACB=60°,求∠BOC的大小.