题目内容
14. 如图,在半径为r的⊙O中,E是劣弧AB的中点,C为优弧AB上的一动点,连EC交AB于点F,EB=$\frac{r}{2}$.
如图,在半径为r的⊙O中,E是劣弧AB的中点,C为优弧AB上的一动点,连EC交AB于点F,EB=$\frac{r}{2}$.(1)D为AB延长线上一点,若DC=DF,证明:直线DC与⊙O相切.
(2)证明:EF•EC为定值.
分析 (1)连接OC、OE,OE交AB于H,如图1,由E是弧AB的中点,根据垂径定理的推论得到OE⊥AB,则∠HEF+∠HFE=90°,由对顶角相等得∠HFE=∠CFD,则∠HEF+∠CFD=90°,再由DC=DF得∠CFD=∠DCF,加上∠OCE=∠OEC,所以∠OCE+∠DCE=∠HEF+∠CFD=90°,于是根据切线的判定定理得直线DC与⊙O相切;
(2)连接BC,由$\widehat{AE}$=$\widehat{BE}$,根据圆周角定理得到∠ABE=∠BCE,证出△EBF∽△ECB,利用相似比得到EF•EC=$\frac{{r}^{2}}{4}$即可.
解答 (1)证明:连结OC、OE,OE交AB于H 如图1所示:
如图1所示:
∵E是弧AB的中点,
∴OE⊥AB,
∴∠EHF=90°,
∴∠HEF+∠HFE=90°,
∵∠HFE=∠CFD,
∴∠HEF+∠CFD=90°,
∵DC=DF,
∴∠CFD=∠DCF,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE+∠DCE=∠HEF+∠CFD=90°,
∴OC⊥CD,
∴直线DC与⊙O相切;
(2)证明:连结BC,如图2所示:
∵E是弧AB的中点,
∴$\widehat{AE}$=$\widehat{BE}$,
∴∠ABE=∠BCE,
∵∠FEB=∠BEC,
∴△EBF∽△ECB,
∴EF:BE=BE:EC,
∴EF•EC=BE2=($\frac{r}{2}$)2=$\frac{{r}^{2}}{4}$;
即EF•EC为定值.
点评 本题考查了切线的判定、相似三角形的判定与性质、垂径定理、圆周角定理等知识;熟练掌握垂径定理及其推论、切线的判定定理和圆周角定理并利用相似三角形的性质是解决问题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
4.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角是( )
| A. | 42°、138° | B. | 都是10° | ||
| C. | 42°、138°或10°、10° | D. | 以上都不对 |
9.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边长为39,那么较大的三角形的面积为( )
| A. | 90 | B. | 180 | C. | 270 | D. | 540 |
19.已知一个正多边形的每个外角都等于72°,则这个正多边形是( )
| A. | 正五边形 | B. | 正六边形 | C. | 正七边形 | D. | 正八边形 |
3.已知关于x的不等式ax>b的解为x<3,那么下列关于x的不等式中解为x>3的是( )
| A. | -2ax>-2b | B. | 2ax>2b | C. | ax+2>b+2 | D. | ax-2>b-2 |
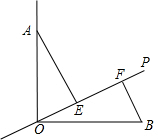 如图,∠AOB=90°,OA=OB,OP是∠AOB内可以绕着点O自由转动的一条射线,分别过点A、B作AE⊥OP、BF⊥OP,垂足分别为点E、F,假设OP从OB出发,绕着点O逆时针转动到OA(OP不与OB、OA重合),转动的角度为α.
如图,∠AOB=90°,OA=OB,OP是∠AOB内可以绕着点O自由转动的一条射线,分别过点A、B作AE⊥OP、BF⊥OP,垂足分别为点E、F,假设OP从OB出发,绕着点O逆时针转动到OA(OP不与OB、OA重合),转动的角度为α.