题目内容
10.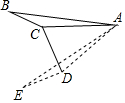 如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子α+β=180°.
如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子α+β=180°.
分析 先过A作AF⊥CD,根据旋转的性质,得出∠ADE=∠ACB=α,AC=AD,∠CAD=2β,再根据等腰三角形的性质,即可得到Rt△ADF中,∠DAF+∠ADF=β+α-90°=90°,据此可得α与β的等量关系.
解答 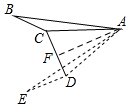 解:如图,过A作AF⊥CD,
解:如图,过A作AF⊥CD,
由旋转可得,∠ADE=∠ACB=α,
∵CD⊥DE,
∴∠ADC=α-90°,
由旋转可得,AC=AD,∠CAD=2β,
∴∠DAF=β,
∴Rt△ADF中,∠DAF+∠ADF=90°,即β+α-90°=90°,
∴α+β=180°.
故答案为:α+β=180°.
点评 本题主要考查了旋转的性质,三角形内角和定理以及等腰三角形的性质的综合应用,解决问题的关键是作辅助线构造直角三角形,依据等腰三角形三线合一的性质进行计算.

练习册系列答案
相关题目
1.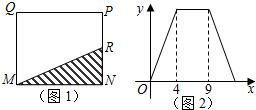 如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停下,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停下,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
 如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停下,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停下,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )| A. | 当x=2时,y=5 | B. | 矩形MNPQ的面积是20 | ||
| C. | 当x=6时,y=10 | D. | 当y=$\frac{15}{2}$时,x=3 |
15.如果代数式x2+kx+49能分解成(x-7)2形式,那么k的值为( )
| A. | 7 | B. | -14 | C. | ±7 | D. | ±14 |

 如图,在正方形ABCD内有一折线段,其中AE丄EF,EF丄FC,并且AE=3,EF=4,FC=5,则正方形ABCD的外接圆的半径是4$\sqrt{5}$.
如图,在正方形ABCD内有一折线段,其中AE丄EF,EF丄FC,并且AE=3,EF=4,FC=5,则正方形ABCD的外接圆的半径是4$\sqrt{5}$.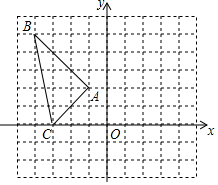 如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,
如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,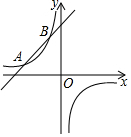 如图,一次函数的图象与反比例函数的图象交于A(-3,1)、B(m,3)两点,
如图,一次函数的图象与反比例函数的图象交于A(-3,1)、B(m,3)两点,