题目内容
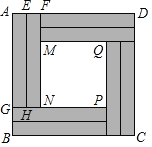
【题目】某公司对自家办公大楼一块![]() 米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形
米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形![]() ,用材料乙装修). 两种材料的成本如下表:
,用材料乙装修). 两种材料的成本如下表:
材料 | 甲 | 乙 |
价格(元/米2) | 550 | 500 |
设矩形的较短边![]() 的长为
的长为![]() 米,装修材料的总费用为
米,装修材料的总费用为![]() 元.
元.
(1)计算中心区的边![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长![]() 不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)预备材料的购买资金32000元不够用,理由见解析
;(3)预备材料的购买资金32000元不够用,理由见解析
【解析】
(1)根据图形边长即可表示出MN的长;
(2)根据正方形和长方形的面积乘以每平方米的单价即可写出函数解析式;
(3)根据题意确定x的取值范围,根据函数的增减性即可得结论.
(1)根据题意,得![]() ,
,
四周阴影部分是八个全等的矩形,
∴![]() .
.
答:中心区的边![]() 的长为
的长为![]() .
.
(2)根据题意,得
![]()
![]() .
.
答:![]() 关于
关于![]() 的函数解析式
的函数解析式![]() .
.
(3)∵![]() 不小于2,
不小于2,
∴![]() ,
,
∴![]() .
.
![]()
![]()
∵![]() ,
,
∴图象开口向下,在对称轴的左侧,![]() 随
随![]() 的增大而增大,
的增大而增大,
∴![]() 时,
时,![]() .
.
而![]() ,
,
答:预备材料的购买资金32000元不够用.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目