题目内容
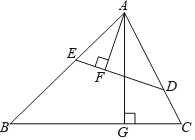
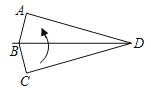
【题目】定义:有一组对角互补的四边形叫做互补四边形,如图,在互补四边形纸片ABCD中,BA=BC,AD=CD,∠A=∠C=90°,∠ADC=30°.将纸片先沿直线BD对折,再将对折后的纸片从一个顶点出发的直线裁剪,把剪开的纸片打开后铺平,若铺平后的纸片中有一个面积为4的平行四边形,则CD的长为__.
【答案】2![]() +4
+4![]() 或
或![]() +2
+2![]() .
.
【解析】
根据题意结合裁剪的方法得出符合题意的图形有两个,分别利用菱形的判定与性质以及勾股定理得出CD的长.
解:如图1所示:从顶点A(或C)剪开纸片,四边形ABCE是平行四边形,
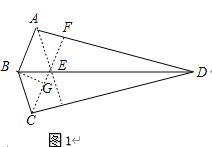
根据题意可知:
∵BA=BC,AD=CD,∠A=∠C=90°
∴△ABD≌△CBD(SAS)
∴∠ABD=∠CBD=75°,
∵四边形ABCE是面积为4的平行四边形,AB=CB
∴ABCE是菱形,
∴△BCE的面积为2,CB=CE=AB,
∴∠BCE=30°,
作BG⊥CE于点G,
∴BC=2BG,
∴CE=2BG,
∴S△BCE=![]() CEBG=2
CEBG=2
∴BG2=2,
∴BG=![]() ,CE=2
,CE=2![]() ,
,
∴CG=![]() BG=
BG=![]() ,
,
∴CF=CG+GF=CG+AB=CG+CE=![]() +2
+2![]() .
.
∵∠ADC=30°,∠CFD=90°
∴CD=2CF=2![]() +4
+4![]() .
.
如图2,从顶点B剪开纸片,当四边形BEDF是平行四边形时,
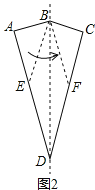
∵BE=BF,
∴平行四边形BEDF是菱形,
∵∠A=∠C=90°,∠B=150°,
∴∠ADB=∠BDC=15°,
∵BE=DE,
∴∠AEB=30°,
∴设AB=y,则BE=2y,AE= ![]() y,
y,
∴DE=2y,
∵四边形BEDF面积为4,
∴AB×DE=4,
即2y2=4,
解得:y=![]() ,
,
故AE=![]() ,DE=2
,DE=2![]() ,
,
则CD=AD=![]() +2
+2![]() ,
,
综上所述:CD的值为:2![]() +4
+4![]() 或
或![]() +2
+2![]() .
.
故答案为2![]() +4
+4![]() 或
或![]() +2
+2![]() .
.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
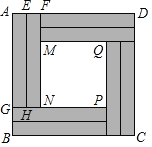
名师点睛字词句段篇系列答案【题目】某公司对自家办公大楼一块![]() 米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形
米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形![]() ,用材料乙装修). 两种材料的成本如下表:
,用材料乙装修). 两种材料的成本如下表:
材料 | 甲 | 乙 |
价格(元/米2) | 550 | 500 |
设矩形的较短边![]() 的长为
的长为![]() 米,装修材料的总费用为
米,装修材料的总费用为![]() 元.
元.
(1)计算中心区的边![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长![]() 不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.