题目内容
14.求当x取何值时,代数式$\frac{3x-5}{7}$-$\frac{x+4}{3}$的值不小于1?分析 根据题意得出不等式,求出不等式的解集即可求得x的取值范围.
解答 解:根据题意得:$\frac{3x-5}{7}$-$\frac{x+4}{3}$≥1,
3(3x-5)-7(x+4)≥21,
9x-15-7x-28≥21,
9x-7x≥21+28+15,
2x≥64,
x≥32.
故当x≥32时,代数式$\frac{3x-5}{7}$-$\frac{x+4}{3}$的值不小于1.
点评 本题考查了解一元一次不等式的应用,解此题的关键是能根据题意得出一元一次不等式,应按照去括号,移项,合并同类项,系数化为1这个步骤来解.

练习册系列答案
相关题目
2.已知|n+2|+(5m-3)2=0,则关于x的方程10mx+4=3x+n的解是x=( )
| A. | 2 | B. | -2 | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
4.从5、6、7、8、9、10这六个数中随机取出一个数,取出的数是2的倍数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
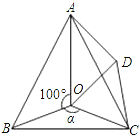 如图,点O是等边△ABC内一点,∠AOB=100°,∠BOC=α,D是△ABC外一点,且△BOC≌△ADC,连接OD.
如图,点O是等边△ABC内一点,∠AOB=100°,∠BOC=α,D是△ABC外一点,且△BOC≌△ADC,连接OD. 如图,已知∠ABC=90°,D是直线AB上的点,AD=BC,如图,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF.
如图,已知∠ABC=90°,D是直线AB上的点,AD=BC,如图,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF. 如图,线段AB=1cm,延长AB到C,使得BC=$\frac{3}{2}$AB,反向延长AB到D,使得BD=2BC,在线段CD上有一点P,且AP=2cm.
如图,线段AB=1cm,延长AB到C,使得BC=$\frac{3}{2}$AB,反向延长AB到D,使得BD=2BC,在线段CD上有一点P,且AP=2cm. 如图在△ABC中,点D、E分别是AB、AC边上的定点,请你在BC边上确定一点P,使△PDE的周长最小(在图中作出点P,保留作图痕迹,不写作法)
如图在△ABC中,点D、E分别是AB、AC边上的定点,请你在BC边上确定一点P,使△PDE的周长最小(在图中作出点P,保留作图痕迹,不写作法)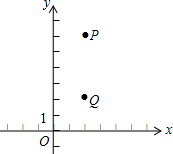 在平面直角坐标系中,P点坐标为(2,6),Q点坐标为(2,2),点M为y轴上的动点.
在平面直角坐标系中,P点坐标为(2,6),Q点坐标为(2,2),点M为y轴上的动点.