题目内容
1.已知三角形两边长分别是3和4,第二边长是方程(2x-11)2-(x-1)2=0的解.(1)求出第三边长;
(2)求出三角形周长;
(3)判断这个三角形的形状;
(4)求出它的面积.
分析 (1)先根据平方差公式分解因式,再解方程,由三角形三边关系确定第三边为4;
(2)计算三边的和即可;
(3)有两边相等,则是等腰三角形
(4)作高线,求高AD的长,代入面积公式可求得结果.
解答 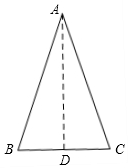 解:(1)(2x-11)2-(x-1)2=0,
解:(1)(2x-11)2-(x-1)2=0,
(2x-11+x-1)(2x-11-x+1)=0,
(3x-12)(x-10)=0,
x=4或10,
∵三角形两边长分别是3和4,
∴1<第三边长<7,
∴x=10不符合题意,舍去,
∴第三边长为4;
(2)三角形周长=3+4+4=11;
(3)∵三角形的三边长分别为3、4、4,
∴此三角形是等腰三角形;
(4)如图,过A作AD⊥BC,垂足为D,
∵AB=AC=4,
∴DC=$\frac{1}{2}$BC=$\frac{1}{2}$×3=$\frac{3}{2}$,
由勾股定理得:AD=$\sqrt{{4}^{2}-(\frac{3}{2})^{2}}$=$\frac{\sqrt{55}}{2}$,
∴S△ABC=$\frac{1}{2}$AD•BC=$\frac{1}{2}$×$\frac{\sqrt{55}}{2}$×3=$\frac{3\sqrt{55}}{4}$,
答:它的面积是$\frac{3\sqrt{55}}{4}$.
点评 本题考查了利用因式分解法解一元二次方程和三角形的三边关系、等腰三角形的判定,属于基础题,难度不大,掌握三角形的两边之和大于第三边,两边之差小于第三边;在解方程时,可以利用平方差公式分解因式求解,也可以利用完全平方公式展开化为一般形式后,再解方程.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
16.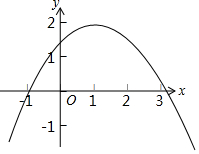 如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )
如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )
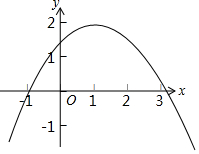 如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )
如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )| A. | abc>0 | B. | 3a-b+c>0 | C. | 2a+b+c>0 | D. | c>-4a |
 如图:梯形ABCD,AD∥BC,对角线AC、BD交于点E,AD=2,BC=3,S△AED=2,则S梯形ABCD=12.5.
如图:梯形ABCD,AD∥BC,对角线AC、BD交于点E,AD=2,BC=3,S△AED=2,则S梯形ABCD=12.5. 如图,已知DE∥AB,EF∥BC,且OD:DA=3:2,则△ABC与△DEF是位似图形,位似比为3:5;△OAB与△OED是位似图形,位似中心是点O.
如图,已知DE∥AB,EF∥BC,且OD:DA=3:2,则△ABC与△DEF是位似图形,位似比为3:5;△OAB与△OED是位似图形,位似中心是点O. 如图,已知:△ABC和直线l,请作出△ABC关于直线l的对称三角形.
如图,已知:△ABC和直线l,请作出△ABC关于直线l的对称三角形.