题目内容
4.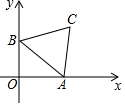 如图,点A,B分别是x轴.y轴上的两个动点,以AB为边作等边△ABC,若AB=2,设点C到原点O的距离为d,则d的取值范围是$\sqrt{3}$-1≤d≤$\sqrt{3}$+1.
如图,点A,B分别是x轴.y轴上的两个动点,以AB为边作等边△ABC,若AB=2,设点C到原点O的距离为d,则d的取值范围是$\sqrt{3}$-1≤d≤$\sqrt{3}$+1.
分析 如图,取AB中点P,连接OP、PC,由OP+PC≥OC,可知当O、P、C共线时,OC的值最大,最大值=$\sqrt{3}$+1;当B位于y轴的负半轴上且AO=BO时,OC最小,最小值为$\sqrt{3}$-1.
解答 解:如图,取AB中点P,连接OP、PC,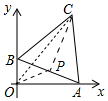
∵OP+PC≥OC,
∴当O、P、C共线时,OC的值最大,此时OP=$\frac{1}{2}$AB,最大值=$\sqrt{3}$+1.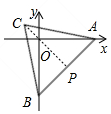
当B在y轴上时,OC最小,最小值为$\sqrt{3}$-1.
∴$\sqrt{3}$-1≤d≤$\sqrt{3}$+1,
故答案为:$\sqrt{3}$-1≤d≤$\sqrt{3}$+1.
点评 此题考查了直角三角形斜边上的中线性质,等边三角形的性质,以及勾股定理的应用,熟练掌握在直角三角形中,斜边上的中线等于斜边的一半是解本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
14.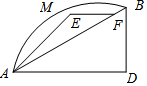 如图所示,某同学的家在A处,星期日他到书店去买书,想尽快赶到书店B,请你帮助他选择一条最近的路线( )
如图所示,某同学的家在A处,星期日他到书店去买书,想尽快赶到书店B,请你帮助他选择一条最近的路线( )
 如图所示,某同学的家在A处,星期日他到书店去买书,想尽快赶到书店B,请你帮助他选择一条最近的路线( )
如图所示,某同学的家在A处,星期日他到书店去买书,想尽快赶到书店B,请你帮助他选择一条最近的路线( )| A. | A→D→B | B. | A→F→B | C. | A→E→F→B | D. | A→M→B |
16.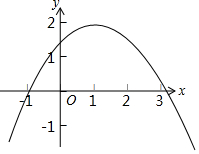 如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )
如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )
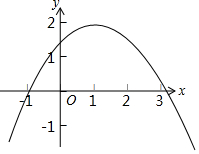 如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )
如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )| A. | abc>0 | B. | 3a-b+c>0 | C. | 2a+b+c>0 | D. | c>-4a |
 如图:梯形ABCD,AD∥BC,对角线AC、BD交于点E,AD=2,BC=3,S△AED=2,则S梯形ABCD=12.5.
如图:梯形ABCD,AD∥BC,对角线AC、BD交于点E,AD=2,BC=3,S△AED=2,则S梯形ABCD=12.5. 如图,已知DE∥AB,EF∥BC,且OD:DA=3:2,则△ABC与△DEF是位似图形,位似比为3:5;△OAB与△OED是位似图形,位似中心是点O.
如图,已知DE∥AB,EF∥BC,且OD:DA=3:2,则△ABC与△DEF是位似图形,位似比为3:5;△OAB与△OED是位似图形,位似中心是点O.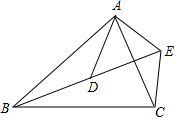 如图,在△ABC中,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$.求证:∠BAD=∠CAE.
如图,在△ABC中,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$.求证:∠BAD=∠CAE.