题目内容
8.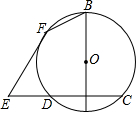 如图,AB是⊙O的直径,$\widehat{AC}$=$\widehat{AD}$,E为弦CD的延长线上一点,EF与⊙O相切于F,若∠E=40°,则∠EFB的度数为160°.
如图,AB是⊙O的直径,$\widehat{AC}$=$\widehat{AD}$,E为弦CD的延长线上一点,EF与⊙O相切于F,若∠E=40°,则∠EFB的度数为160°.
分析 连接OF,如图,先利用垂径定理的推论得到∠OGD=90°,再根据切线的性质得∠EFO=90°,则根据四边形的内角和得到∠AOF=140°,然后根据等腰三角形的性质和三角形外角性质可计算出∠OFB=70°,最后计算∠OFE+∠OFB即可.
解答 解:连接OF,如图,
∵$\widehat{AC}$=$\widehat{AD}$,
∴AB⊥CD,
∴∠OGD=90°,
∵EF为切线,
∴OF⊥EF,
∴∠EFO=90°,
∴∠AOF+∠E=180°,
∴∠AOF=180°-40°=140°,
∵OB=OF,
∴∠B=∠OFB,
∴∠AOF=∠B+∠OFB,
∴∠OFB=70°,
∴∠EFB=∠OFE+∠OFB=90°+70°=160°.
故答案为160°.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
16.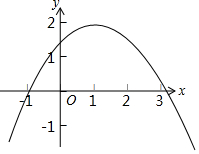 如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )
如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )
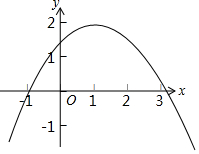 如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )
如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )| A. | abc>0 | B. | 3a-b+c>0 | C. | 2a+b+c>0 | D. | c>-4a |