��Ŀ����
3��̽����Ӧ�ã�̽����һ��أ�����һ����ʽ��һԪ���η���ax2+bx+c=0��a��0������b2-4ac��0ʱ�����ĸ���x=$\frac{-b��\sqrt{{b}^{2}-4ac}}{2a}$ ��b2-4ac��0����
���x1��x2��һԪ���η��� ax2+bx+c=0��a��0��������������ôx1+x2=-$\frac{b}{a}$��x1•x2=$\frac{c}{a}$�������ú�a��b��c�Ĵ���ʽ��ʾ��
Ӧ�ã���֪x1��x2�Ƿ���2x2+4x-3=0��������������̽����õĸ���ϵ����ϵ��
��1����գ�x1+x2=-2��x1•x2=-$\frac{3}{2}$��
��2����ֵ����x1+1����x2+1����
���� ̽�������ݷ��̵Ľ�Ϊ$\frac{-b��\sqrt{{b}^{2}-4ac}}{2a}$���������x1+x2��x1•x2�У������ɵó����ۣ�
Ӧ�ã���1�����ݸ���ϵ���Ĺ�ϵ��Ϸ��̸���ϵ�������ɵó�x1+x2��x1•x2��ֵ��
��2������x1+1����x2+1��չ�����ٴ���x1+x2��x1•x2��ֵ����������ۣ�
��� �⣺̽������x=$\frac{-b��\sqrt{{b}^{2}-4ac}}{2a}$��
��x1+x2=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$+$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$=-$\frac{b}{a}$��x1•x2=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$��$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{c}{a}$��
�ʴ�Ϊ��-$\frac{b}{a}$��$\frac{c}{a}$��
Ӧ�ã���1����x1��x2�Ƿ���2x2+4x-3=0����������
��x1+x2=-$\frac{4}{2}$=-2��x1•x2=$\frac{-3}{2}$=-$\frac{3}{2}$��
�ʴ�Ϊ��-2��-$\frac{3}{2}$��
��2����x1+1����x2+1��=x1•x2+��x1+x2��+1=-$\frac{3}{2}$-2+1=-$\frac{5}{2}$��
���� ���⿼���˸���ϵ���Ĺ�ϵ��������������֮��Ϊ-$\frac{b}{a}$������֮��Ϊ$\frac{c}{a}$�ǽ���Ĺؼ���

 �û��������з�ʽ������Σ�
�û��������з�ʽ������Σ���1�������
| ������� | 1 | 2 | 3 | 4 | �� |
| �������� | 3 | 5 | 7 | 9 | �� |
��3����n=1 008ʱ�������ĸ����Ƕ��٣�
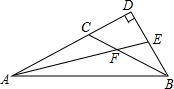 ��ͼ���ڡ�ABC�У���CAB=��ABC=$\frac{1}{4}$��ACB��AF�ǡ�CAB��ƽ���ߣ��ӳ�AF��AC���ϵĸ�BD�ڵ�E�����AEB�Ķ�����
��ͼ���ڡ�ABC�У���CAB=��ABC=$\frac{1}{4}$��ACB��AF�ǡ�CAB��ƽ���ߣ��ӳ�AF��AC���ϵĸ�BD�ڵ�E�����AEB�Ķ�����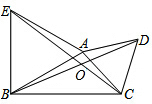 ��ͼ���ڡ�ABC�У��ֱ���AB��ACΪ�����ȱ�������ABE��ACD��BD��CE�ཻ�ڵ�O��
��ͼ���ڡ�ABC�У��ֱ���AB��ACΪ�����ȱ�������ABE��ACD��BD��CE�ཻ�ڵ�O��