题目内容
12.如图,已知在Rt△ABC中,AB=BC,AC=6,∠ABC=90°,点P是AC边上有一点D,使PB=PD.(1)当点P运动到AC中点时,求BP的长;
(2)若∠BPD=45°,请证明:AC=AB+CD;
(3)如图,过点D作DE⊥线段AC于E.
①试猜想线段PE与AC的数量关系,并说明理由.
②当AP=3-$\sqrt{3}$时,∠BPD为30°.(直接写出答案)
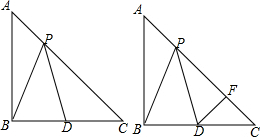
分析 (1)过B作BO⊥AC于O,当点P运动到AC中点时,即点P与O重合,于是得到PB=BO,根据等腰直角三角形的性质即可得到结论;
(2)根据等腰三角形的性质得到∠PBD=∠PDB=62.5°,由∠C=45°,得到∠BPC=∠PDB=62.5°,推出AB=PC,证得△ABP≌△PCD,根据全等三角形的性质得到AP=CD,即可得到结论;
(3)①PE=$\frac{1}{2}$AC,根据等腰三角形的性质得到∠2=∠PBD,由等腰直角三角形的性质得到∠C=45°,求得∠1=45°,推出∠3=∠4,证得△BPO≌△PDE,根据全等三角形的性质和等腰三角形的性质即可得到结论;②根据等腰三角形的性质得到∠1=45°,得到∠3=30°,根据三角函数得到OP=$\frac{\sqrt{3}}{3}$BO=$\sqrt{3}$,即可得到结论.
解答 解:(1)过B作BO⊥AC于O,
当点P运动到AC中点时,即点P与O重合,
∴PB=BO,
∵△ABC是等腰直角三角形,
∴PB=BO=$\frac{1}{2}$AC=3;
(2)∵∠BPD=45°,
PB=PD,
∴∠PBD=∠PDB=62.5°,
∵∠C=45°,
∴∠BPC=∠PDB=62.5°,
∴BC=PC,∠APB=∠PDC,
∴AB=PC,
在△ABP与△PDC中,
$\left\{\begin{array}{l}{∠A=∠C}\\{∠APB=∠PDC}\\{AB=PC}\end{array}\right.$,
∴△ABP≌△PCD,
∴AP=CD,
∴AC=AP+PC=AB+CD;
(3)①PE=$\frac{1}{2}$AC,
∵PB=PD,
∴∠2=∠PBD,
∵AB=BC,∠ABC=90°,
∴∠C=45°,
∵BO⊥AC,
∴∠1=45°,
∴∠1=∠C=45°,
∵∠3=∠PBO-∠1,∠4=∠2-∠C,
∴∠3=∠4,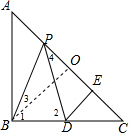
∵BO⊥AC,DE⊥AC,
∴∠BOP=∠PED=90°,
在△BPO和△PDE中
$\left\{\begin{array}{l}{∠3=∠4}\\{∠BOP=∠PED}\\{PB=PD}\end{array}\right.$,
∴△BPO≌△PDE,
∴PE=BO=$\frac{1}{2}$AC;
②∵∠BPD=30°,
∴∠PBD=∠PDB=75°,
∵∠1=45°,
∴∠3=30°,
∴OP=$\frac{\sqrt{3}}{3}$BO=$\sqrt{3}$,
∴AP=OA-OP=3-$\sqrt{3}$.
∴当AP=3-$\sqrt{3}$时,∠BPD为30°.
故答案为:3-$\sqrt{3}$.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,等腰三角形的性质,熟练掌握全等三角形的性质是解题的关键.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案| A. | -1 | B. | 1 | C. | -2或0 | D. | ±1 |
| A. | 4x2y+4y2x=8x2y | B. | 2abc+2ab=4ab | C. | 7ab-3ba=4ab | D. | a3+a2=a5 |
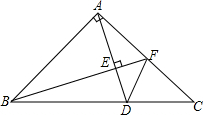 已知△ABC,AB=AC,∠BAC=90°,点F在AC的中点,AD⊥BF,垂足为E,若DE=2,则△ADF的面积为$\frac{15}{4}$.
已知△ABC,AB=AC,∠BAC=90°,点F在AC的中点,AD⊥BF,垂足为E,若DE=2,则△ADF的面积为$\frac{15}{4}$.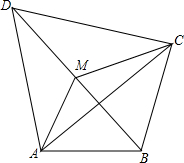 如图,已知四边形ABCD,M是BD的中点.
如图,已知四边形ABCD,M是BD的中点.