题目内容
17.某公司主要生产和销售A产品,每件产品的成本为200元,销售单价为260元,顾客一次购买A产品不超过10件,每件销售为260元;若一次购买A型产品多于10件,则每多一件,所购买的全部产品的销售单价均降低2元,但销售单价均不低于224元.(1)顾客一次购买A产品多少件时,销售单价恰好为224元?
(2)某次交易中,小张一次性购买A产品x件,公司盈利792元,求本次交易中小张购买产品的件数.
(3)进入冬季,公司举行“情系山区,你我共同送温暖”的公益促销活动,活动规定:在原定价格的基础上每件均优惠5元,若一次购买A型产品不超过10件,则每销售一件产品公司捐款5元;若一次购买A型产品超过10件,则每售出一件产品公司捐款a元,此外再一次性捐款100元,受活动影响,每位顾客购买件数x均满足10<x≤17,为使顾客一次购买的数量越多,公司在该次交易中所获得的利润越大,求a的取值范围.
分析 (1)根据一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低2元,得出260-2(x-10)=224求出即可;
(2)根据利润关系式,列出一元二次方程,求出件数;
(3)由于此次购买数量大于10件,根据已知,设利润为y,根据条件列出二次函数关系式,利用对称轴性质求出a的取值范围.
解答 解:(1)设商家一次购买该产品x件时,销售单价恰好为224元.
260-2(x-10)=224,
解得:x=28;
答:顾客一次购买A产品28件时,销售单价恰好为224元.
(2)设本次交易中小张购买产品的件数是x,
∵792>(260-200)×10,
∴x>10,
根据题意得:[260-2(x-10)-200]x=792,
解得:x1=22,x2=18,
∴本次交易中小张购买产品的件数是22件或18件;
(3)设公司获利为y,则y=[260-2(x-10)-5-a-200]x-100,
即y=-2x2+(75-a)x-100,对称轴x=-$\frac{75-a}{-4}$=$\frac{75-a}{4}$,
∵顾客一次购买的数量越多,公司在该次交易中所获得的利润越大,
$\frac{75-a}{4}$≥17
解得:a≤7,
∴a的取值范围为:0≤a≤7.
点评 此题主要考查了二次函数的应用以及二次函数最值问题,根据已知建立函数关系式,借助二次函数解决实际问题是解题关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
14.如果等腰三角形的顶角等于40°,那么它的一个底角为( )
| A. | 40° | B. | 70° | C. | 40°或70° | D. | 不能确定 |
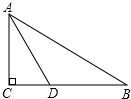 如图所示,在△ABC中,∠C=90°,D点在线段AB的中垂线上,BC=6cm,BD=5cm,那么△ABC的周长是6+2$\sqrt{6}$+2$\sqrt{15}$cm.
如图所示,在△ABC中,∠C=90°,D点在线段AB的中垂线上,BC=6cm,BD=5cm,那么△ABC的周长是6+2$\sqrt{6}$+2$\sqrt{15}$cm.