题目内容
8.已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=1,且经过点(-3,y1),(3,y2),试比较y1和y2的大小:y1>y2(填“>”,“<”或“=”)分析 由于二次函数y=ax2+bx+c的图象的开口向上,对称轴为直线x=1,然后根据点A(-3,y1)和点B(3,y2)离对称轴的远近可判断y1与y2的大小关系.
解答 解:∵二次函数y=ax2+bx+c的图象的对称轴为直线x=1,
而1-(-3)=4,3-1=2,
∴点(-1,y1)离对称轴的距离比点(2,y2)要远,
∴y1>y2.
故答案为>.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足解析式y=ax2+bx+c(a、b、c为常数,a≠0).

练习册系列答案
相关题目
16.已知O半径为3,A为线段PO的中点,则当OP=7时,点A与O的位置关系为( )
| A. | 点在圆内 | B. | 点在圆上 | C. | 点在圆外 | D. | 不能确定 |
13.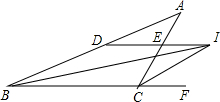 如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )
如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )
 如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )
如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )| A. | 2cm | B. | 5cm | C. | 4cm | D. | 5cm |
17.已知x=1是关于x的方程2x-a=0的解,则a的值是( )
| A. | -5 | B. | 5 | C. | 7 | D. | 2 |
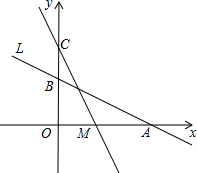 如图,直线L:y=-$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
如图,直线L:y=-$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.