题目内容
1.化简(1)$\frac{{3{x^2}{y^2}}}{{2{a^2}{b^2}}}{(-\frac{{{b^{\;}}}}{x})^2}÷\frac{{3{y^2}x}}{{4a{b^{\;}}}}$
(2)请你先化简,再选取一个使原分式有意义,而你又喜欢的数代入求值:$\frac{{{x^3}-{x^2}}}{{{x^2}-x}}$.
分析 (1)直接根据分式混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,求出x的值代入进行计算即可.
解答 解:(1)原式=$\frac{3{x}^{2}{y}^{2}}{2{a}^{2}{b}^{2}}$•$\frac{{b}^{2}}{{x}^{2}}$•$\frac{4ab}{3{y}^{2}x}$
=$\frac{3{y}^{2}}{2{a}^{2}}$•$\frac{4ab}{3{y}^{2}x}$
=$\frac{2b}{ax}$;
(2)原式=$\frac{{x}^{2}(x-1)}{x(x-1)}$
=x,
当x=2时,原式=2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
6.如图,将一直角三角板与纸条的两边如图所示放置,下列条件:
(1)∠1=∠2;(2)∠3=∠4;(3)∠2+∠4=90°;(4)∠4+∠5=180°,
能说明纸条两边平行其中正确的个数有( )
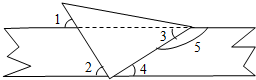
(1)∠1=∠2;(2)∠3=∠4;(3)∠2+∠4=90°;(4)∠4+∠5=180°,
能说明纸条两边平行其中正确的个数有( )

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.下列命题中的真命题是( )
| A. | 菱形是中心对称图形,但不是轴对称图形 | |
| B. | 相等的弦所对应的弦心距相等 | |
| C. | 直角三角形的外心和重心之间的距离等于斜边的六分之一 | |
| D. | 三角形的内心是三角形三边的中垂线的交点 |
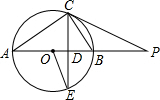 如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连结OE、AC,已知∠POE=2∠CAB,∠P=∠E.
如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连结OE、AC,已知∠POE=2∠CAB,∠P=∠E.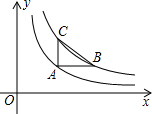 如图,已知点A在反比例函数y=$\frac{2}{x}$的图象上,点B,C分别在反比例函数y=$\frac{4}{x}$的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为(2,1).
如图,已知点A在反比例函数y=$\frac{2}{x}$的图象上,点B,C分别在反比例函数y=$\frac{4}{x}$的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为(2,1).