题目内容
11.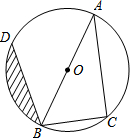 已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.(1)求BD的长;
已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.(1)求BD的长;(2)求图中阴影部分的面积.
分析 (1)由AB为⊙O的直径,得到∠ACB=90°,由勾股定理求得AB,OB=5cm.连OD,得到等腰直角三角形,根据勾股定理即可得到结论;
(2)根据S阴影=S扇形-S△OBD即可得到结论.
解答 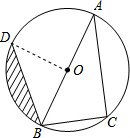 解:(1)∵AB为⊙O的直径,
解:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∵BC=6cm,AC=8cm,
∴AB=10cm.
∴OB=5cm.
连OD,
∵OD=OB,
∴∠ODB=∠ABD=45°.
∴∠BOD=90°.
∴BD=$\sqrt{O{B}^{2}+O{D}^{2}}$=5$\sqrt{2}$cm.
(2)S阴影=S扇形-S△OBD=$\frac{90}{360}$π•52-$\frac{1}{2}$×5×5=$\frac{25π-50}{4}$cm2.
点评 本题考查了圆周角定理,勾股定理,等腰直角三角形的性质,扇形的面积,三角形的面积,连接OD构造直角三角形是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
1.从A地向B地打长途电话,通话时间不超过3min收费2.4元,超过3min后每分加收1元.
(Ⅰ)根据题意,填写下表:
(Ⅱ)设通话时间为xmin,通话费用y元,求y与x的函数解析式;
(Ⅲ)若小红有10元钱,求她打一次电话最多可以通话的时间(本题中通话时间取整数,不足1min的通话时间按1min计费).
(Ⅰ)根据题意,填写下表:
| 通话时间min | 2 | 3 | 6 | … |
| 通话费用/元 | 2.4 | 2.4 | 5.4 | … |
(Ⅲ)若小红有10元钱,求她打一次电话最多可以通话的时间(本题中通话时间取整数,不足1min的通话时间按1min计费).
19.今年江苏省参加高考的人数约为393000人,这个数据用科学记数法可表示为( )
| A. | 393×103 | B. | 3.93×103 | C. | 3.93×105 | D. | 3.93×106 |
3.某市七天的空气质量指数分别是:28,45,28,45,28,30,53,这组数据的众数是( )
| A. | 28 | B. | 30 | C. | 45 | D. | 53 |
20.下列四个图形中是正方体的平面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
12.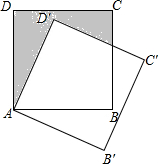 如图,边长为1的正方形ABCD绕点A顺时针旋转30°到AB′C′D′的位置,则图中阴影部分的面积为( )
如图,边长为1的正方形ABCD绕点A顺时针旋转30°到AB′C′D′的位置,则图中阴影部分的面积为( )
 如图,边长为1的正方形ABCD绕点A顺时针旋转30°到AB′C′D′的位置,则图中阴影部分的面积为( )
如图,边长为1的正方形ABCD绕点A顺时针旋转30°到AB′C′D′的位置,则图中阴影部分的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 1-$\frac{\sqrt{3}}{3}$ | D. | 1-$\frac{\sqrt{3}}{4}$ |
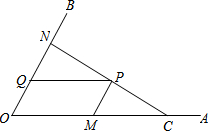 如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.