题目内容
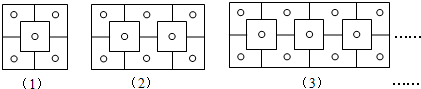
下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第n个图中所贴剪纸“○”的个数为( )

| A、3n | B、3n+1 |
| C、3n+2 | D、3n+3 |
考点:规律型:图形的变化类
专题:
分析:观察图形可知从第二个图案开始,第加一扇窗户,就增加3个剪纸.照此规律便可计算出第n个图形中剪纸的个数.
解答:解:第一个图案为3+2=5个窗花;
第二个图案为2×3+2=8个窗花;
第三个图案为3×3+2=11个窗花;
…从而可以探究:
第n个图案所贴窗花数为(3n+2)个.
故选C.
第二个图案为2×3+2=8个窗花;
第三个图案为3×3+2=11个窗花;
…从而可以探究:
第n个图案所贴窗花数为(3n+2)个.
故选C.
点评:本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
相关题目
下列计算正确的是( )
| A、2x2•3x3=6x6 |
| B、x3÷x3=0 |
| C、(2xy)3=6x3y3 |
| D、(x3)m÷x2m=xm |
 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )
如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )| A、20° | B、30° |
| C、40° | D、60° |