题目内容
一次函数的图象经过点A(0,3),且与两条坐标轴截得的直角三角形的面积为6,求这个一次函数的解析式.
考点:待定系数法求一次函数解析式
专题:
分析:分一次函数与x轴交点Q在正半轴与负半轴两种情况确定出Q的坐标,即可确定出一次函数解析式.
解答:解:①当一次函数与x轴交点Q在x轴负半轴时,
由OP=3,与两坐标所围成的直角三角形面积为6,得到Q(-4,0),
设一次函数解析式为y=kx+b,
将P与Q坐标代入得:
,
解得:k=
,b=-4,此时一次函数解析式为y=
x+3;
当一次函数与x轴交点在x轴正半轴时,
由OP=3,与两坐标所围成的直角三角形面积为6,得到Q(4,0),
设一次函数解析式为y=mx+n,
将P与Q坐标代入得:
,
解得:k=-
,b=-4,此时一次函数解析式为y=-
x+3.
由OP=3,与两坐标所围成的直角三角形面积为6,得到Q(-4,0),
设一次函数解析式为y=kx+b,
将P与Q坐标代入得:
|
解得:k=
| 3 |
| 4 |
| 3 |
| 4 |
当一次函数与x轴交点在x轴正半轴时,
由OP=3,与两坐标所围成的直角三角形面积为6,得到Q(4,0),
设一次函数解析式为y=mx+n,
将P与Q坐标代入得:
|
解得:k=-
| 3 |
| 4 |
| 3 |
| 4 |
点评:此题考查了待定系数法求一次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
下列等式能够成立的是 ( )
| A、(x-y)2=(-x-y)2 |
| B、(x-y)2=(y-x)2 |
| C、(m-n)2=m2-n2 |
| D、(m+n)2=m2+n2 |
下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第n个图中所贴剪纸“○”的个数为( )
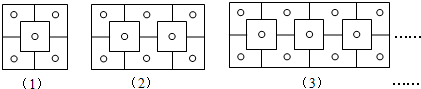

| A、3n | B、3n+1 |
| C、3n+2 | D、3n+3 |
新华商场销售某种冰箱,每台进价为2500元,销售价为2900元,平均每天能售出8台;调查发现,当销售价每降低50元,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱应该降价多少元?若设每台冰箱降价x元,根据题意可列方程( )
A、(2900-x)(8+4×
| ||
B、(400-x)(8+4×
| ||
C、4(2900-x)(8+
| ||
D、4(400-x)(8+
|
下列各组单项式中是同类项的为( )
| A、3xy,3xyz |
| B、2ab2c,2a2bc |
| C、-x2y2,7y2x2 |
| D、5a,-ab |