题目内容
6.下列各组数中,是二元一次方程3x-y=5的解的是( )| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
分析 二元一次方程3x-y=5的解有无数个,所以此题应该用排除法确定答案,分别代入方程组,使方程左右相等的解才是方程组的解.
解答 解:A、把x=1,y=2代入方程,左边=3-2=1≠右边,所以不是方程的解;
B、把x=-1,y=2代入方程,左边=-3-2=-5≠右边,所以不是方程的解;
C、把x=-2,y=1代入方程,左边=-6-1=-7≠右边,所以不是方程的解;
D、把x=2,y=1代入方程,左边=6-1=5=右边,所以是方程的解.
故选D.
点评 本题考查二元一次方程的解的定义,要求理解什么是二元一次方程的解,并会把x,y的值代入原方程验证二元一次方程的解.

练习册系列答案
相关题目
16.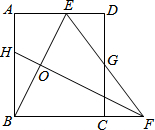 如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,以下几个结论:
如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,以下几个结论:
①∠AEB=∠BEF;②△BEF是等腰三角形;③△DEG与△BEF相似;④四边形ABCD的面积为56.
则以上正确的有( )
 如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,以下几个结论:
如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,以下几个结论:①∠AEB=∠BEF;②△BEF是等腰三角形;③△DEG与△BEF相似;④四边形ABCD的面积为56.
则以上正确的有( )
| A. | ①③ | B. | ②③④ | C. | ①② | D. | ①②④ |
14.甲、乙两人每次都从五个数-2,-1,0,1,2中任取一个,分别记作(x,y),则这些坐标表示的点在直线y=x+1上的概率为( )
| A. | $\frac{4}{25}$ | B. | $\frac{8}{25}$ | C. | $\frac{9}{25}$ | D. | $\frac{2}{5}$ |
1. 如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
 如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
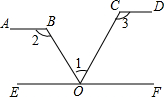
如图,如果AB∥EF,EF∥CD,下列各式正确的是( )| A. | ∠1+∠2-∠3=90° | B. | ∠1-∠2+∠3=90° | C. | ∠1+∠2+∠3=90° | D. | ∠2+∠3-∠1=180° |
15.下列计算正确的是( )
| A. | -x2+3x2=2 | B. | x2×x3=x6 | ||
| C. | (x+1)(-x-1)=-x2-2x-1 | D. | $\frac{{x}^{2}-4}{x-2}$=x-2 |
16.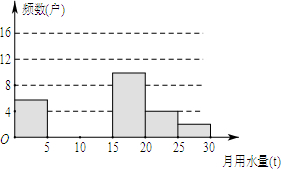 某校社会活动实践小组的同学们为了解2015年教工小区家庭月平均用水情况,随机调查了该小区部分家庭,并将调查数据整理成如下的统计表和直方图
某校社会活动实践小组的同学们为了解2015年教工小区家庭月平均用水情况,随机调查了该小区部分家庭,并将调查数据整理成如下的统计表和直方图
根据上述的数据整理信息,请解答以下问题:
(1)求出统计表中m,n的值;
(2)把频数分布直方图补充完整;
(3)若该小区有1500户家庭,根据调查数据估计,该小区月平均用水量超过20t的家庭大约有多少户?
 某校社会活动实践小组的同学们为了解2015年教工小区家庭月平均用水情况,随机调查了该小区部分家庭,并将调查数据整理成如下的统计表和直方图
某校社会活动实践小组的同学们为了解2015年教工小区家庭月平均用水情况,随机调查了该小区部分家庭,并将调查数据整理成如下的统计表和直方图| 月平均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | m | 0.24 |
| 10<x≤15 | n | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | k |
| 25<x≤30 | 2 | 0.04 |
(1)求出统计表中m,n的值;
(2)把频数分布直方图补充完整;
(3)若该小区有1500户家庭,根据调查数据估计,该小区月平均用水量超过20t的家庭大约有多少户?
 将如图方格纸中的线段AB平移,分别画出经下列平移后所得的图形:
将如图方格纸中的线段AB平移,分别画出经下列平移后所得的图形: