题目内容
20.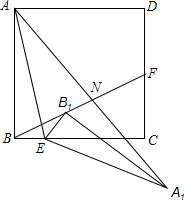 如图,正方形ABCD中,AB=4,点E是BC上靠近点B的四等分点,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在点A1位置处,连接AA1交BF于点N,则AN的长为$\frac{2\sqrt{85}}{5}$.
如图,正方形ABCD中,AB=4,点E是BC上靠近点B的四等分点,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在点A1位置处,连接AA1交BF于点N,则AN的长为$\frac{2\sqrt{85}}{5}$.
分析 先找出辅助线判断出点P是BB1的中点,由旋转得到△BPE∽△BCF,再判断出A,B1,M三点共线,再由B1Q=$\frac{4\sqrt{5}}{5}$,A1Q=$\frac{8\sqrt{5}}{5}$=AB1最后用勾股定理计算即可.
解答 解:如图,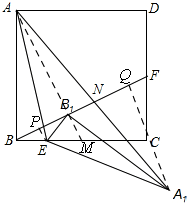
作EP⊥BF,A1Q⊥BF,取BC的中点M,连接AB1,B1M,
∴点P是BB1的中点,
∵E是BM中点,
∴EP∥MB1,
∴MB1⊥BB1,
由旋转得,△BPE∽△BCF,
∴BP=$\frac{2\sqrt{5}}{5}$,EP=$\frac{\sqrt{5}}{5}$,
∵PB1=PB=$\frac{2\sqrt{5}}{5}$,
∴BB1=$\frac{4\sqrt{5}}{5}$,
∵sin∠FBC=$\frac{CF}{BF}$=$\frac{\sqrt{5}}{5}$=$\frac{B{B}_{1}}{BA}$,
∴∠AB1B=90°,
∴A,B1,M三点共线,
∴AB1=$\frac{8\sqrt{5}}{5}$,
∵∠B1A1Q=∠BB1E=∠FBC,
∴△B1QA1∽△FCB,
∴B1Q=$\frac{4\sqrt{5}}{5}$,A1Q=$\frac{8\sqrt{5}}{5}$=AB1,
∴△AB1N≌△A1QN,
∴B1N=$\frac{1}{2}$B1Q=$\frac{2\sqrt{5}}{5}$,
根据勾股定理得,AN=$\frac{2\sqrt{85}}{5}$,
故答案为:$\frac{2\sqrt{85}}{5}$.
点评 此题是旋转性质题,主要考查了等腰三角形的性质,相似三角形的性质和判定,全等三角形的判定和性质,锐角三角函数的意义,解本题的关键是作出辅助线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.一艘轮船在静水中的最大航速为30km/h,它以最大航速沿江顺流航行90km所用时间,与以最大航速逆流航行60km所用时间相等.设江水的流速为vkm/h,根据题意,下列所列方程正确的是( )
| A. | $\frac{90}{30+v}=\frac{60}{30-v}$ | B. | $\frac{90}{v}=\frac{60}{30-v}$ | C. | $\frac{90}{30-v}=\frac{60}{30+v}$ | D. | $\frac{90}{30-v}=\frac{60}{v}$ |
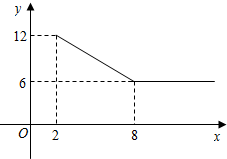 某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图所示;B类杨梅深加工后再销售,深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图所示;B类杨梅深加工后再销售,深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
 如图,已知AB是⊙O的直径,OD⊥AC,OD=3,则弦BC的长为6.
如图,已知AB是⊙O的直径,OD⊥AC,OD=3,则弦BC的长为6.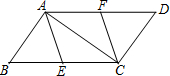 如图,已知点E,F分别是?ABCD的边BC、AD上的中点,且∠BAC=90°,
如图,已知点E,F分别是?ABCD的边BC、AD上的中点,且∠BAC=90°,