题目内容
19. 如图,在平面直角坐标系中,△ABC的面积为24,OA=OB,BC=12,求
如图,在平面直角坐标系中,△ABC的面积为24,OA=OB,BC=12,求(1)△ABC三个顶点的坐标;
(2)△ABC的周长.
分析 (1)根据△ABC的面积为24,得出$\frac{1}{2}$×12×AO=24,求得AO=4,即可得出A(0,4),B(-4,0),C(8,0);
(2)先根据勾股定理求得AB、AC的长,再计算△ABC的周长.
解答  解:(1)∵△ABC的面积为24,BC=12,
解:(1)∵△ABC的面积为24,BC=12,
∴$\frac{1}{2}$×12×AO=24,
解得AO=4,
∴OA=OB=4,CO=12=4-8,
∴A(0,4),B(-4,0),C(8,0);
(2)在Rt△AOB中,AB=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
Rt△AOC中,AC=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
∴△ABC的周长=12+4$\sqrt{2}$+4 $\sqrt{5}$.
点评 本题主要考查了三角形的面积、勾股定理的运用,解决问题的关键是掌握:三角形的面积等于底边长与高线乘积的一半;在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
10. 实数a,b在数轴上的位置如图所示,下列各式正确的是( )
实数a,b在数轴上的位置如图所示,下列各式正确的是( )
 实数a,b在数轴上的位置如图所示,下列各式正确的是( )
实数a,b在数轴上的位置如图所示,下列各式正确的是( )| A. | a>0 | B. | b<0 | C. | a>b | D. | |a|>|b| |
7.下列方程中,是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | 2x+y=0 | C. | x2+1=0 | D. | x2+y=3 |
14.已知a>0,b<0,且a的绝对值小于b的绝对值,则直线y=ax+b和直线y=bx+a相交于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a5 | C. | a3÷a3=0 | D. | (a3)2=a9 |
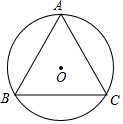 如图,等边△ABC内接于⊙O,已知⊙O的半径为4,则边长BC的长为4$\sqrt{3}$.
如图,等边△ABC内接于⊙O,已知⊙O的半径为4,则边长BC的长为4$\sqrt{3}$.