题目内容
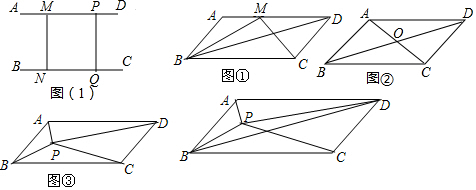
19.我们知道:平行线间的距离处处相等,即:如图(1)已知AD∥BC,MN⊥AD,PQ⊥AD,所以PQ=MN.已知:图①~④中的四边形ABCD都是平行四边形(其中AD∥BC,AD=BC,AB∥CD,AB=CD,)设它的面积为S.
(1)如图①,点M为AD边上任意一点,则△BCM的面积S1=$\frac{1}{2}$S,△BCD的面积S2与△BCM的面积S1的数量关系是S1=S2;
(2)如图②,设AC、BD交于点O,则O为AC、BD的中点,则△AOD的面积S3与四边形ABCD的面积S的数量关系是S3=$\frac{1}{4}$S.
(3)如图③,点P为平行四边形ABCD内任意一点时,记△PAD的面积为S4,△PBC的面积为S5,猜想得S4、S5的和与四边形ABCD的面积为S的数量关系式为S4+S5=$\frac{1}{2}$S.
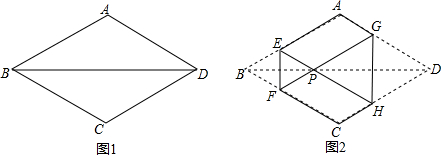
(4)如图④,已知点P为平行四边形ABCD内任意一点,△PA2的面积为2,△PDC的面积为4,求△PBD的面积.
分析 (1)设?ABCD中BC边上的高为h1,CD边上的高为h2,根据平行四边形的面积公式,三角形的面积公式分别计算即可解决问题;
(2)结论:S3=$\frac{1}{4}$S,如图②中,在平行四边形ABCD中,O为AC、BD的中点,可得S△AOD=S△AOB=S△BOC=S△ODC,由此即可解决问题;
(3)如图③中设?ABCD中BC边上的高为h2,△PBC中BC边上高为h3,△PAD中AD边上的高为h4,再根据平行四边形的面积与三角形的面积公式求解即可;
(4)根据S△PBD=S四边形PBCD-S△BCD=S△PBC+S△PCD-S△BCD,计算即可;
解答 解:(1)如图①中,设?ABCD中BC边上的高为h1,CD边上的高为h2,
∵S?ABCD=BC•h1=CD•h2=S,
S△BCM=$\frac{1}{2}$BC•h1=$\frac{1}{2}$S,S△BCD=$\frac{1}{2}$CD•h2=$\frac{1}{2}$S,
∴S1=$\frac{1}{2}$S,S1=S2(或相等).
故答案为:$\frac{1}{2}$;S1=S2;
(2)S3=$\frac{1}{4}$S
理由:如图②中,∵O为AC、BD的中点,
∴S△AOD=S△AOB=S△BOC=S△ODC
∴S3=$\frac{1}{4}$S;
故答案为S3=$\frac{1}{4}$S;
(3)如图③中设?ABCD中BC边上的高为h2,△PBC中BC边上高为h3,△PAD中AD边上的高为h4,
∵AD∥BC,
∴h3+h4=h2,
∴S△PAD+S△PCB=$\frac{1}{2}$BC•h3+$\frac{1}{2}$AD•h4=$\frac{1}{2}$BC(h3+h4)=$\frac{1}{2}$BC•h2=$\frac{1}{2}$S,即S4+S5=$\frac{1}{2}$S;
故答案为:S4+S5=$\frac{1}{2}$S;
(4)∵S△PBC+S△PAD=$\frac{1}{2}$S=S△BCD,S△PAD=2,S△PCD=4,
∴S△PBD=S四边形PBCD-S△BCD=S△PBC+S△PCD-S△BCD,即S△PBD=4+( $\frac{1}{2}$S-2)-$\frac{1}{2}$S=4-2=2.
点评 本题考查的是平行四边形的性质,熟知平行四边形及三角形的面积公式是解答此题的关键,学会利用参数解决问题,属于中考压轴题.

| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | 2-$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
| A. | 如果m是实数,那么m是有理数 | B. | -5没有立方根 | ||
| C. | 互补的角一定的邻补角 | D. | 正数不全是有理数 |
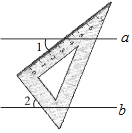 已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )
已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )| A. | 37° | B. | 53° | C. | 63° | D. | 27° |
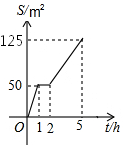 园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )
园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )| A. | 75m2 | B. | 50m2 | C. | 31.25m2 | D. | 25m2 |
 如图,已知AB⊥BC,BD⊥AC,EC⊥AC,∠1与∠2互补,试说明DF⊥BC的理由.
如图,已知AB⊥BC,BD⊥AC,EC⊥AC,∠1与∠2互补,试说明DF⊥BC的理由.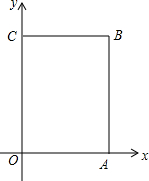 已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动)
已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动)