题目内容
18. 如图,已知矩形ABCD(AB<AD).
如图,已知矩形ABCD(AB<AD).(1)请用直尺和圆规按下列步骤作图,保留作图痕迹;
①以点A为圆心,以AD的长为半径画弧交边BC于点E,连接AE;
②作∠DAE的平分线交CD于点F;
③连接EF;
(2)在(1)作出的图形中,若AB=8,AD=10,则tan∠FEC的值为$\frac{3}{4}$.
分析 (1)根据题目要求作图即可;
(2)由(1)知AE=AD=10、∠DAF=∠EAF,可证△DAF≌△EAF得∠D=∠AEF=90°,即可得∠FEC=∠BAE,从而由tan∠FEC=tan∠BAE=$\frac{BE}{AB}$可得答案.
解答 解:(1)如图所示;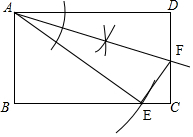
(2)由(1)知AE=AD=10、∠DAF=∠EAF,
∵AB=8,
∴BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=6,
在△DAF和△EAF中,
∵$\left\{\begin{array}{l}{AD=AE}\\{∠DAF=∠EAF}\\{AF=AF}\end{array}\right.$,
∴△DAF≌△EAF(SAS),
∴∠D=∠AEF=90°,
∴∠BEA+∠FEC=90°,
又∵∠BEA+∠BAE=90°,
∴∠FEC=∠BAE,
∴tan∠FEC=tan∠BAE=$\frac{BE}{AB}$=$\frac{6}{8}$=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 本题主要考查作图-基本作图及全等三角形的判定与性质、解直角三角形,熟练掌握角平分线的尺规作图和全等三角形的判定与性质是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
9.计算-1+2的结果是( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
6.将抛物线y=2(x-4)2-1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )
| A. | y=2x2+1 | B. | y=2x2-3 | C. | y=2(x-8)2+1 | D. | y=2(x-8)2-3 |
13.-$\frac{1}{3}$的绝对值是( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
3.在创建“全国园林城市”期间,郴州市某中学组织共青团员去植树,其中七位同学植树的棵树分别为:3,1,1,3,2,3,2,这组数据的中位数和众数分别是( )
| A. | 3,2 | B. | 2,3 | C. | 2,2 | D. | 3,3 |
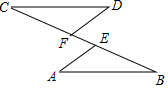 如图,点C、F、E、B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.
如图,点C、F、E、B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.
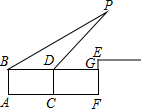 某学校组织数学兴趣小组的学生,进行一次课外数学实践探究活动,活动课题:利用直角三角形的边角关系,测量“底部不可以到达的旗杆高度”,活动的方式:两个人一个小组,测量后全班交流研讨,活动工具:测倾器,长度相同的标杆若干,皮尺等测量工具,已知领操台EM距地面的高EF为2m,标杆的长为1.6m,甲乙两人分在一组,测量步骤如下:
某学校组织数学兴趣小组的学生,进行一次课外数学实践探究活动,活动课题:利用直角三角形的边角关系,测量“底部不可以到达的旗杆高度”,活动的方式:两个人一个小组,测量后全班交流研讨,活动工具:测倾器,长度相同的标杆若干,皮尺等测量工具,已知领操台EM距地面的高EF为2m,标杆的长为1.6m,甲乙两人分在一组,测量步骤如下: