题目内容
18.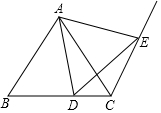 如图,△ABC是等边三角形,点D是BC上的点,点E是射线CN上的点,且CN∥AB,联结AD、AE、DE
如图,△ABC是等边三角形,点D是BC上的点,点E是射线CN上的点,且CN∥AB,联结AD、AE、DE(1)当∠DAE=60°时,求证:∠ADE是等边三角形;
(2)当∠ADE=60°时,“△ADE是等边三角形”还成立吗?若成立请证明,若不成立,说明理由.
分析 (1)根据等腰三角形的性质得到AB=AC,∠BAC=∠B=60°,由平行线的性质得到∠ACE=∠BAC,等量代换得到∠BAD=∠CAE,根据全等三角形的性质得到AD=AE,于是得到结论;
(2)在AB上截取AM=CD,连接DM,得到△BDM是等边三角形,求得∠BMD=∠BDM=60°根据三角形的内角和和平角的定义得到∠1=∠2,推出∠AMD=∠DCE=120°,根据全等三角形的性质得到AD=DE,于是得到结论.
解答 (1)证明:△ABC是等边三角形,
∴AB=AC,∠BAC=∠B=60°,
∵CN∥AB,
∴∠ACE=∠BAC,
∴∠B=∠ACE,
∵∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD与△ACE中,$\left\{\begin{array}{l}{∠B=∠ACE}\\{AB=AC}\\{∠BAD=∠CAE}\end{array}\right.$,
∴△ABD≌△ACE,
∴AD=AE,
∴△DAC是等边三角形;
(2)成立,在AB上截取AM=CD,连接DM,
∵AB=BC,
∴BM=BD,
∵∠B=60°,
∴△BDM是等边三角形,
∴∠BMD=∠BDM=60°,
∴∠AMD=120°,
∴∠1+∠ADB=180°-60°=120°,
∠2+∠ADB=120°,
∴∠1=∠2,
∵CN∥AB,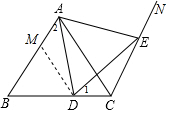
∴∠ACE=∠BAC=60°,
∴∠AMD=∠DCE=120°,
在△AMD与△DEC中$\left\{\begin{array}{l}{∠2=∠1}\\{AM=DC}\\{∠AMD=∠DCE}\end{array}\right.$,
∴△AMD≌△DCE,
∴AD=DE,
∵∠DAE=60°,
∴△ADE是等边三角形.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,平行线的性质,正确的作出辅助线构造全等三角形是解题的关键.

| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
| A. | 正三角形 | B. | 正方形 | C. | 正六边形 | D. | 正八边形 |
| A. | x≥1 | B. | x≠-2 | C. | x≥1且x≠-2 | D. | x≠1 |
 如图,已知BC是以AB为直径的⊙O的切线,且BC=AB,连接OC交⊙O于点D,延长AD交BC于点E,F为BE的中点.
如图,已知BC是以AB为直径的⊙O的切线,且BC=AB,连接OC交⊙O于点D,延长AD交BC于点E,F为BE的中点.
 如图,已知抛物线与x轴只有一个交点A(-2,0),与y轴交于点B(0,4).
如图,已知抛物线与x轴只有一个交点A(-2,0),与y轴交于点B(0,4).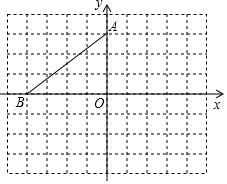 在平面直角坐标系中,点A、B的坐标分别是(0,3)、(-4,0),
在平面直角坐标系中,点A、B的坐标分别是(0,3)、(-4,0),