题目内容
8. 如图,已知BC是以AB为直径的⊙O的切线,且BC=AB,连接OC交⊙O于点D,延长AD交BC于点E,F为BE的中点.
如图,已知BC是以AB为直径的⊙O的切线,且BC=AB,连接OC交⊙O于点D,延长AD交BC于点E,F为BE的中点.(1)求证:DF是⊙O的切线;
(2)若OB=1,求DF的长.
分析 (1)连接BD,根据等边对等角可得∠FDB=∠FBD,∠ODB=∠OBD,然后根据切线的性质即可证得;
(2)证明△CDF∽△CBO,利用相似三角形的对应边的比相等求得BC的长,然后在直角△OBC中利用勾股定理求解.
解答 (1)证明:连接BD,
∵AB是直径,
∴∠BDA=90°,
∴∠BDE=90°,
又∵F为BE的中点,
∴EF=BF=DF,
∴∠FBD=∠FDB,
∵OD=OB,
∴∠ODB=∠OBD,
∵BC是⊙O的切线,AB是直径,
∴AB⊥BC,
∴∠FBD+∠OBD=90°,
∴∠FDO=∠FDB+∠ODB=∠FBD+∠OBD=90°,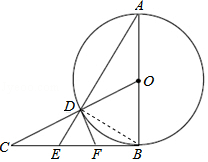
∴OD⊥DF,
∴DF是圆的切线;
(2)解:在△CDF和△CBO中
∵∠FDO═∠CBO,
∠C=∠C
∴△CDF∽△CBO,
∴$\frac{DF}{OB}$=$\frac{CD}{CB}$,
∵BC=AB=2OB=2,
∴DF=$\frac{1}{2}$CD,
在直角△OBC中,由勾股定理得,OC=$\sqrt{C{B}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴CD=$\sqrt{5}$-1,
∴DF=$\frac{1}{2}$CD=$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了切线的判定,等腰三角形的性质等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
17.抛物线y=(x-2016)2+2017的顶点坐标是( )
| A. | (2016,-2017) | B. | (-2016,2017) | C. | (2016,2017) | D. | (-2016,-2017) |
18.下列命题正确的是( )
| A. | 菱形的对角线互相平分 | |
| B. | 顺次连接菱形各边中点得到的四边形是正方形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 顺次连接矩形各边中点得到的四边形是正方形 |
13.直角三角形两直角边长为a,b,斜边上高为h,则下列各式总能成立的是( )
| A. | ab=h2 | B. | a2+b2=2h2 | C. | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{h}$ | D. | $\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$ |
20.若a,b,c为△ABC的三边长,且满足|a-5|+(b-3)2=0,则c的值可以为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
17.已知点P(-3,2)是反比例函数图象上的一 点,则该反比例函数的表达式为( )
| A. | y=$\frac{3}{x}$ | B. | y=-$\frac{5}{x}$ | C. | y=$\frac{6}{x}$ | D. | y=-$\frac{6}{x}$ |
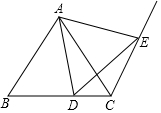 如图,△ABC是等边三角形,点D是BC上的点,点E是射线CN上的点,且CN∥AB,联结AD、AE、DE
如图,△ABC是等边三角形,点D是BC上的点,点E是射线CN上的点,且CN∥AB,联结AD、AE、DE