题目内容
7.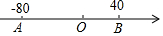 如图,在一条东西方向的马路上O为路边的车站台,A,B两人分别在距离站台东西两侧的80米和40米处,设向东为正,A,B两人各自以一定的速度在马路上行走.且A的行走速度为2米/秒.
如图,在一条东西方向的马路上O为路边的车站台,A,B两人分别在距离站台东西两侧的80米和40米处,设向东为正,A,B两人各自以一定的速度在马路上行走.且A的行走速度为2米/秒.(1)若点A,B两人同时出发相向而行,在O处相遇.
①求B的行走速度;
②设有一条狗在他们两们之间不停的往返跑(即狗遇到A后返回向B跑,遇到B后返回向A跑),直到A、B相遇为止,设狗的速度为4米/秒,问A,B两人相遇时,狗跑了多少米的路程?
(2)若A,B两人以(1)问中各自的速度同时出发,向东运动,几秒钟时两人相距50米;
(3)若A,B两人以(1)问中各自的速度同时出发,向西运动,与此同时,第三个人C从O点出发作同方向的运动,且在运动过程中,始终有$\frac{CA}{CB}$=$\frac{4}{3}$,若干秒钟后,C停留在站台西100米处,求此时B的位置?
分析 (1)①根据速度=路程÷时间,代入数据即可求出结论;②根据时间=路程÷速度可算出二者相遇的时间,再根据路程=速度×时间即可算出狗跑的路程;
(2)设A,B两人以(1)问中各自的速度同时出发,向东运动,x秒钟时两人相距50米,依照A、B的速度找出此时A、B对应的数,再根据两点间的距离公式即可找出关于x的一元一次方程,解之即可得出结论;
(3)设若干秒钟后,C停留在距站台西100米处,此时点B对应的数为(-80-2y),则点A对应的数为(40-y),由此可得出CA、CB的长度,再结合$\frac{CA}{CB}$=$\frac{4}{3}$即可找出关于y的分式方程,解之经检验后即可得出y值,将其代入B对应的数即可得出结论.
解答 解:(1)①B的行走速度为40÷(80÷2)=1(米/秒).
②A,B两人从出发到相遇的时间为80÷2=40(秒),
狗跑的路程为4×40=160(米).
(2)设A,B两人以(1)问中各自的速度同时出发,向东运动,x秒钟时两人相距50米,
此时点A对应的数为2x-80,点B对应的数为40+x,
根据题意得:(40+x)-(2x-80)=±50,
解得:x=70或x=170.
答:A,B两人以(1)问中各自的速度同时出发,向东运动,70秒钟或170秒钟时两人相距50米.
(3)设若干秒钟后,C停留在距站台西100米处,此时点B对应的数为(-80-2y),则点A对应的数为(40-y),
∴CA=40-y-(-100)=140-y,CB=-100-(-80-2y)=2y-20,
∵$\frac{CA}{CB}$=$\frac{4}{3}$,
∴$\frac{140-y}{2y-20}$=$\frac{4}{3}$,
解得:y=$\frac{500}{11}$,
经检验y=$\frac{500}{11}$是方程$\frac{140-y}{2y-20}$=$\frac{4}{3}$的解,
∴-80-2y=-$\frac{1880}{11}$.
答:若干秒钟后,C停留在站台西100米处,求此时B在站台西$\frac{1880}{11}$米处.
点评 本题考查了一元一次方程的应用、数轴以及两点间的距离,根据A、B运动的方向及速度找出点A、B对应的数是解题的关键.

 寒假学与练系列答案
寒假学与练系列答案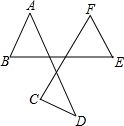 如图,A、B、C、D、E、F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
如图,A、B、C、D、E、F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )| A. | 180° | B. | 360° | C. | 540° | D. | 720° |
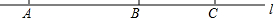 如图所示,点A、B、C在直线l上,则下列说法正确的是( )
如图所示,点A、B、C在直线l上,则下列说法正确的是( )| A. | 图中有2条线段 | B. | 图中有6条射线 | ||
| C. | 点C在直线AB的延长线上 | D. | A、B两点之间的距离是线段AB |
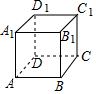 如图,已知正方体的棱长为2,则正方体表面上从A点到C点的最短距离为2$\sqrt{2}$.
如图,已知正方体的棱长为2,则正方体表面上从A点到C点的最短距离为2$\sqrt{2}$. 如图所示,∠A+∠B+∠C+∠D+∠E=180°.
如图所示,∠A+∠B+∠C+∠D+∠E=180°.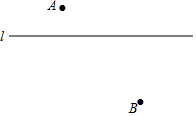 尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B.
尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B.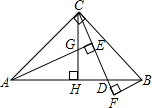 如图,在等腰Rt△ABC中,∠C=90°,D是斜边上AB上任一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,CH⊥AB于H点,交AE于G.
如图,在等腰Rt△ABC中,∠C=90°,D是斜边上AB上任一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,CH⊥AB于H点,交AE于G.