题目内容
3.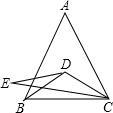 如图,在△ABC中,AB=AC,∠A=50°,D为△ABC内一点,连接BD,CD,E为△ABC外一点,连接CE,DE,已知BD=CD,E=AB,CD平分∠ECA.
如图,在△ABC中,AB=AC,∠A=50°,D为△ABC内一点,连接BD,CD,E为△ABC外一点,连接CE,DE,已知BD=CD,E=AB,CD平分∠ECA.(1)试判断点D是否在∠A的平分线上,并说明理由;
(2)求∠E的度数.
分析 (1)点D在∠A的平分线上,连接AD,证明△ABD≌△ACD,即可解答;
(2)证明△ECD≌△ACD,即可解答.
解答 解:(1)点D在∠A的平分线上.
如图,连接AD,
在△ABD和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\\{BD=CD}\end{array}\right.$
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴点D在∠A的平分线上.
(2)∵点D在∠A的平分线上.
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=25°,
∵CE=AB,AB=AC,
∴CE=AC,
∵CD平分∠ECA,
∴∠ECD=∠ACD,
在△ECD和△ACD中,
$\left\{\begin{array}{l}{EC=AC}\\{∠ECD=∠ACD}\\{CD=CD}\end{array}\right.$
∴△ECD≌△ACD,
∴∠E=∠CAD=25°.
点评 本题考查了全等三角形的性质与定理,解决本题的关键是证明三角形全等.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
13.在9,$\sqrt{3}$,$\frac{3}{16}$,-0.1这四个数中,是无理数的是( )
| A. | 9 | B. | $\sqrt{3}$ | C. | $\frac{3}{16}$ | D. | -0.1 |
18.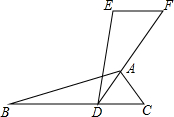 如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
 如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )| A. | 50° | B. | 60° | C. | 100° | D. | 120° |
 如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为$\frac{4}{5}$.
如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为$\frac{4}{5}$.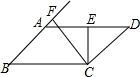 如图,?ABCD中,CE⊥AD于点E,CF⊥BA交BA的延长线于点F,∠FBC=30°,CE=3cm,CF=5cm,求?ABCD的周长.
如图,?ABCD中,CE⊥AD于点E,CF⊥BA交BA的延长线于点F,∠FBC=30°,CE=3cm,CF=5cm,求?ABCD的周长.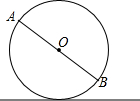 如图,⊙O沿直线l滚动.已知⊙O的半径是0.4m,AB是⊙O的一条直径,当⊙O沿地面滚动时,点A,B到l的距离之和是否改变?若改变,请说明理由;若不改变,请求出点A,B到l的距离之和.
如图,⊙O沿直线l滚动.已知⊙O的半径是0.4m,AB是⊙O的一条直径,当⊙O沿地面滚动时,点A,B到l的距离之和是否改变?若改变,请说明理由;若不改变,请求出点A,B到l的距离之和.