题目内容
8.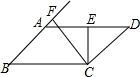 如图,?ABCD中,CE⊥AD于点E,CF⊥BA交BA的延长线于点F,∠FBC=30°,CE=3cm,CF=5cm,求?ABCD的周长.
如图,?ABCD中,CE⊥AD于点E,CF⊥BA交BA的延长线于点F,∠FBC=30°,CE=3cm,CF=5cm,求?ABCD的周长.
分析 由平行四边形的性质可知:∠FBC=∠D=30°,由含30°直角三角形的性质可求得DC=6,BC=10,然后利用平行四边形的性质可求得它的周长.
解答 解:∵CE⊥AD,CF⊥BA,
∴∠BFC=∠CED=90°.
∴△BCF和△CED是直角三角形.
∵四边形ABCD是平行四边形,
∴∠FBC=∠D=30°,AB=CD,AD=BC.
∵在Rt△BCF中,∠FBC=30°.
∴BC=2FC=10cm.
∵在Rt△CED中,∠D=30°.
∴DC=2EC=6cm.
∴?ABCD的周长=2(CD+BC)=2×16=32cm.
点评 本题主要考查的是平行四边形的性质、含30°直角三角形的性质,利用含30°直角三角形的性质求得BC、DC的长是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知2m-n=3,则-4m+2n+5的值为( )
| A. | -1 | B. | 1 | C. | -11 | D. | 11 |
16. 2015年8月31日慧聪网报道,爱唱响内蒙音乐夏令营9月开启,某学校组织部分学生参加夏令营,李老师从夏令营咨询处带回如图所示的两条信息,则原来报名参加夏令营的学生有( )
2015年8月31日慧聪网报道,爱唱响内蒙音乐夏令营9月开启,某学校组织部分学生参加夏令营,李老师从夏令营咨询处带回如图所示的两条信息,则原来报名参加夏令营的学生有( )
 2015年8月31日慧聪网报道,爱唱响内蒙音乐夏令营9月开启,某学校组织部分学生参加夏令营,李老师从夏令营咨询处带回如图所示的两条信息,则原来报名参加夏令营的学生有( )
2015年8月31日慧聪网报道,爱唱响内蒙音乐夏令营9月开启,某学校组织部分学生参加夏令营,李老师从夏令营咨询处带回如图所示的两条信息,则原来报名参加夏令营的学生有( )| A. | 100人 | B. | 150人 | C. | 200人 | D. | 250人 |
17.若A=-2x2+2x+2,B=-3x2+1+2x,则A与B的大小关系是( )
| A. | A>B | B. | A=B | C. | A<B | D. | 无法确定 |
 实数a,b,c在数轴上的对应关系如图,化简下面的式子:|a-b|-|c-a|+|b-c|+|a|.
实数a,b,c在数轴上的对应关系如图,化简下面的式子:|a-b|-|c-a|+|b-c|+|a|.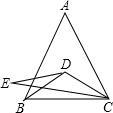 如图,在△ABC中,AB=AC,∠A=50°,D为△ABC内一点,连接BD,CD,E为△ABC外一点,连接CE,DE,已知BD=CD,E=AB,CD平分∠ECA.
如图,在△ABC中,AB=AC,∠A=50°,D为△ABC内一点,连接BD,CD,E为△ABC外一点,连接CE,DE,已知BD=CD,E=AB,CD平分∠ECA. 如图.已知点B,O,D在同一直线上,∠AOB=15°.∠AOC=90°.OE是△DOC的平分线.求∠COE的度数.
如图.已知点B,O,D在同一直线上,∠AOB=15°.∠AOC=90°.OE是△DOC的平分线.求∠COE的度数.