题目内容
若x2+5x+4=(x-1)2+A(x-1)+B恒成立,则A+2B= .
考点:整式的混合运算
专题:
分析:首先去括号,进而合并同类项,得出关于A,B的等式求出即可.
解答:解:∵x2+5x+4=(x-1)2+A(x-1)+B,
∴x2+5x+4
=(x-1)2+A(x-1)+B
=x2-2x+1+Ax-A+B
=x2-(2-A)x+B-A+1
∴-(2-A)=5,B-A+1=4,
解得:A=7,B=10,
则A+2B=7+2×10=27.
故答案为:27.
∴x2+5x+4
=(x-1)2+A(x-1)+B
=x2-2x+1+Ax-A+B
=x2-(2-A)x+B-A+1
∴-(2-A)=5,B-A+1=4,
解得:A=7,B=10,
则A+2B=7+2×10=27.
故答案为:27.
点评:此题主要考查了整式的混合运算,得出关于A,B的等式是解题关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
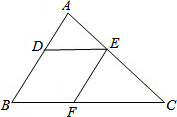 如图,在△ABC中,D、E、F分别是AB、AC、BC上的点,且DE∥BC,EF∥AB,AD:DB=2:3,BC=20cm,求BF的长.
如图,在△ABC中,D、E、F分别是AB、AC、BC上的点,且DE∥BC,EF∥AB,AD:DB=2:3,BC=20cm,求BF的长. 在△ABC中,∠C=90°,AC=6,BC=8,DE垂直平分AB,求BE的长.
在△ABC中,∠C=90°,AC=6,BC=8,DE垂直平分AB,求BE的长.